Neal Grantham
Statistical Rethinking homework solutions with Turing.jl
using Distributions # v0.25
using LinearAlgebra
using ParetoSmooth
using DataFrames # v1.3
using StatsPlots # v0.14
using BSplines
using Turing # v0.19
using CSV # v0.9
standardize(x) = (x .- mean(x)) ./ std(x);
Homework 1
1. Suppose the globe tossing data (Chapter 2) had turned out to be 4 water and 11 land. Construct the posterior distribution, using grid approximation. Use the same flat prior as in the book.
w = 4;
l = 11;
p_grid = range(0, 1, length=1000);
prior_grid = pdf.(Uniform(0, 1), p_grid);
like_grid = pdf.(Binomial.(w + l, p_grid), w);
post_grid = like_grid .* prior_grid;
post_grid /= sum(post_grid);
plot(p_grid, post_grid, ylab="Density", xlab="p", legend=false)
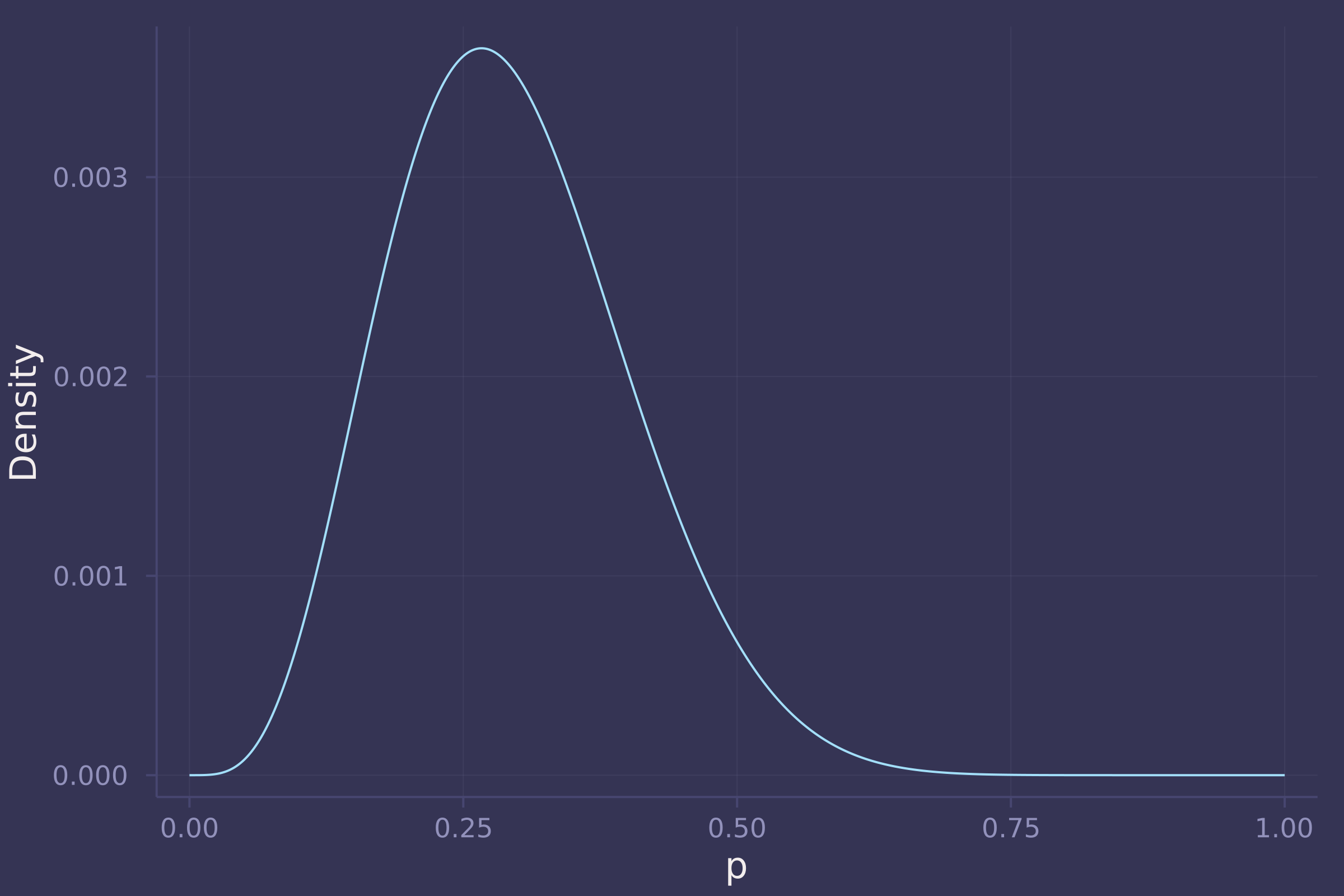
2. Now suppose the data are 4 water and 2 land. Compute the posterior again, but this time use a prior that is zero below p = 0.5 and a constant above p = 0.5. This corresponds to prior information that a majority of the Earth’s surface is water.
w = 4;
l = 2;
prior_grid = pdf.(Uniform(0.5, 1.), p_grid);
like_grid = pdf.(Binomial.(w + l, p_grid), w);
post_grid = like_grid .* prior_grid;
post_grid /= sum(post_grid);
plot(p_grid, post_grid, ylab="Density", xlab="p", legend=false)
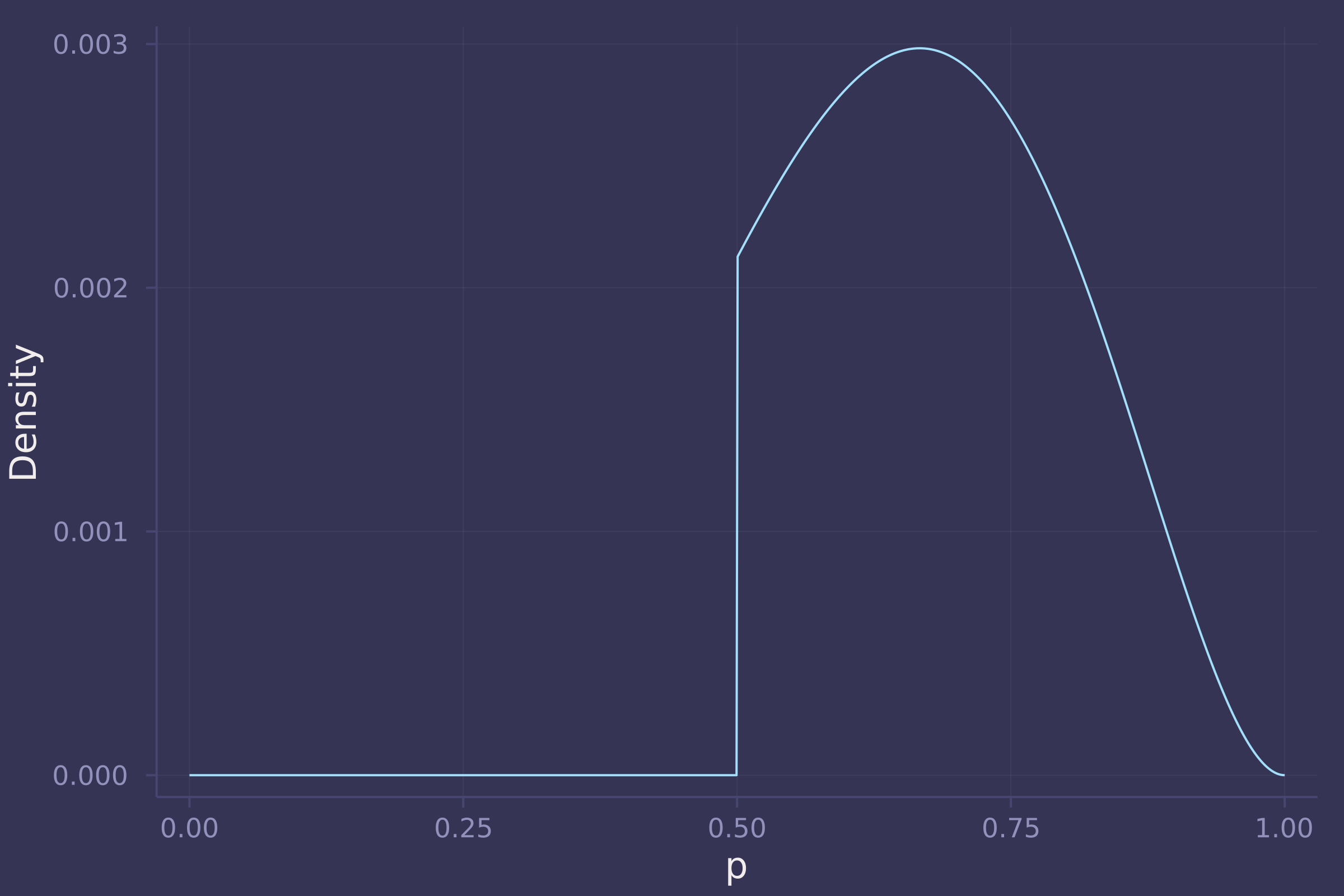
3. For the posterior distribution from 2, compute 89% percentile and HPDI intervals. Compare the widths of these intervals. Which is wider? Why? If you had only the information in the interval, what might you misunderstand about the shape of the posterior distribution?
@model function globetoss(n, w)
p ~ Uniform(0.5, 1.)
w ~ Binomial(n, p)
end;
post = sample(globetoss(w + l, w), MH(), 10_000);
quantile(post, q=[0.055, 0.945])
## Quantiles
## parameters 5.5% 94.5%
## Symbol Float64 Float64
##
## p 0.5243 0.8790
hpd(post, alpha=0.11)
## HPD
## parameters lower upper
## Symbol Float64 Float64
##
## p 0.5002 0.8427
The 89% percentile interval is wider than the 89% HPD interval because the 89% HPD interval is, by definition, the narrowest region with 89% of the posterior probability. If we only had information in the interval, we might completely miss the fact that the distribution is truncated on 0.5 to 1.0!
OPTIONAL CHALLENGE. Suppose there is bias in sampling so that Land is more likely than Water to be recorded. Specifically, assume that 1-in-5 (20%) of Water samples are accidentally recorded instead as Land. First, write a generative simulation of this sampling process. Assuming the true proportion of Water is 0.70, what proportion does your simulation tend to produce instead? Second, using a simulated sample of 20 tosses, compute the unbiased posterior distribution of the true proportion of Water.
If the true proportion of Water is 0.7, and the proportion of Water samples that are accurately recorded as Water is 0.8, then we expect the simulation to tend to produce a proportion of Water of 0.7 * 0.8 = 0.56.
BiasedBinomial(n, p) = Binomial(n, 0.8p);
@model function globetoss(n, w)
p ~ Uniform(0, 1)
w ~ BiasedBinomial(n, p)
end;
n = 20;
w = 11;
post = sample(globetoss(n, w), MH(), 10_000)
## Chains MCMC chain (10000×2×1 Array{Float64, 3}):
##
## Iterations = 1:1:10000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 0.32 seconds
## Compute duration = 0.32 seconds
## parameters = p
## internals = lp
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## p 0.6804 0.1284 0.0013 0.0022 3381.0880 1.0003 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## p 0.4259 0.5913 0.6838 0.7695 0.9247
density(post)
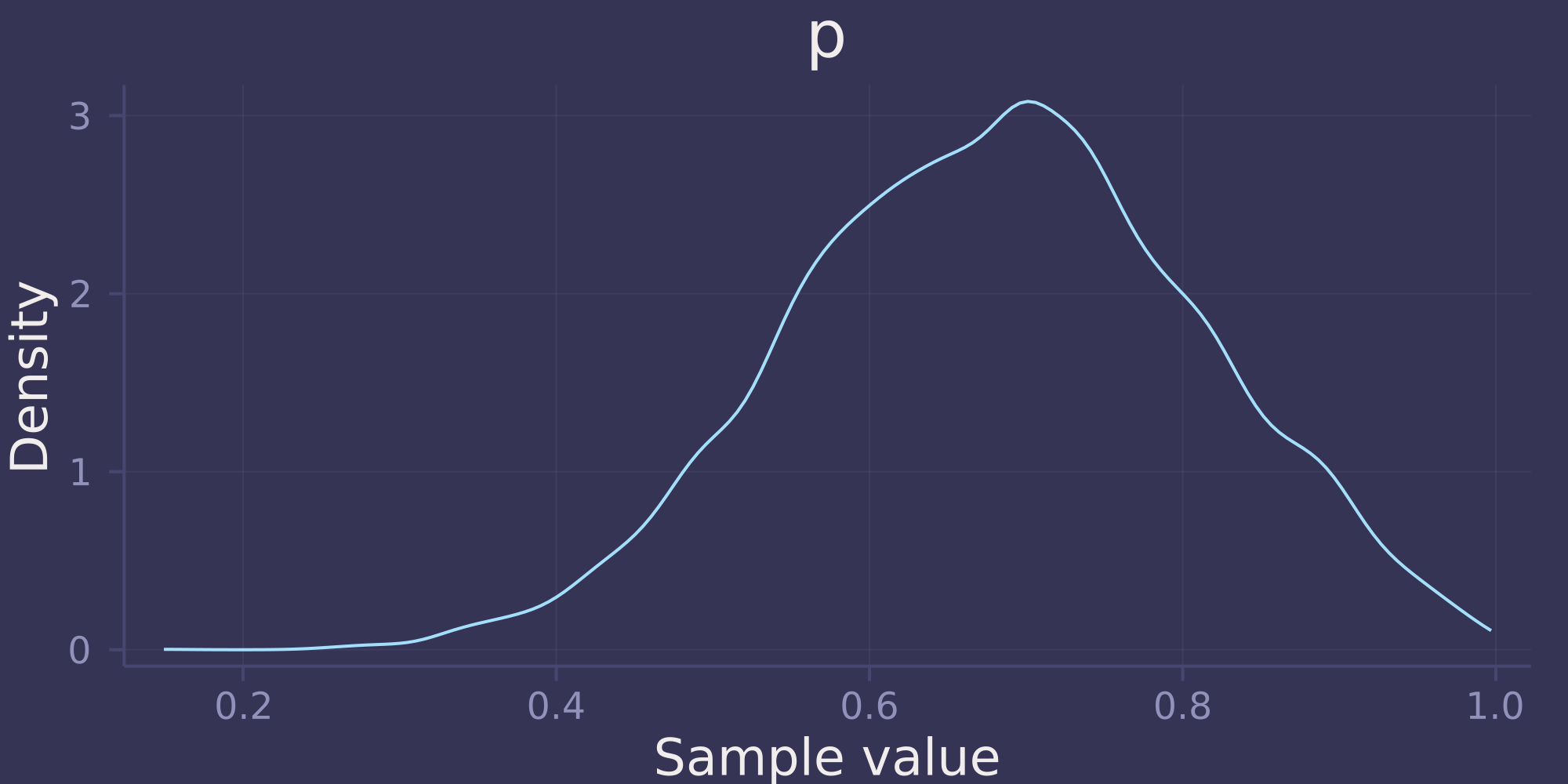
Notice that the posterior distribution is unbiased. Despite recording 11 Water out of 20 tosses (55% Water), the posterior distribution is concentrated around 0.7, the true proportion of Water.
Homework 2
1. Construct a linear regression of weight as predicted by height, using the adults (age 18 or greater) from the Howell1 dataset. The heights listed below were recorded in the !Kung census, but weights were not recorded for these individuals. Provide predicted weights and 89% compatibility intervals for each of these individuals. That is, fill in the table below, using model-based predictions.
| i | height | expected weight | 89% interval |
|---|---|---|---|
| 1 | 140 | ||
| 2 | 160 | ||
| 3 | 175 |
howell = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/Howell1.csv"),
DataFrame,
delim=';'
)
## 544×4 DataFrame
## Row │ height weight age male
## │ Float64 Float64 Float64 Int64
## ─────┼───────────────────────────────────
## 1 │ 151.765 47.8256 63.0 1
## 2 │ 139.7 36.4858 63.0 0
## 3 │ 136.525 31.8648 65.0 0
## 4 │ 156.845 53.0419 41.0 1
## 5 │ 145.415 41.2769 51.0 0
## 6 │ 163.83 62.9926 35.0 1
## 7 │ 149.225 38.2435 32.0 0
## 8 │ 168.91 55.48 27.0 1
## ⋮ │ ⋮ ⋮ ⋮ ⋮
## 538 │ 142.875 34.2462 31.0 0
## 539 │ 76.835 8.02291 1.0 1
## 540 │ 145.415 31.1278 17.0 1
## 541 │ 162.56 52.1631 31.0 1
## 542 │ 156.21 54.0625 21.0 0
## 543 │ 71.12 8.05126 0.0 1
## 544 │ 158.75 52.5316 68.0 1
## 529 rows omitted
adult = howell[howell.age .>= 18, :];
plot(adult.height, adult.weight, ylab="Adult Weight (kg)", xlab="Adult Height (cm)", seriestype=:scatter, legend=false)
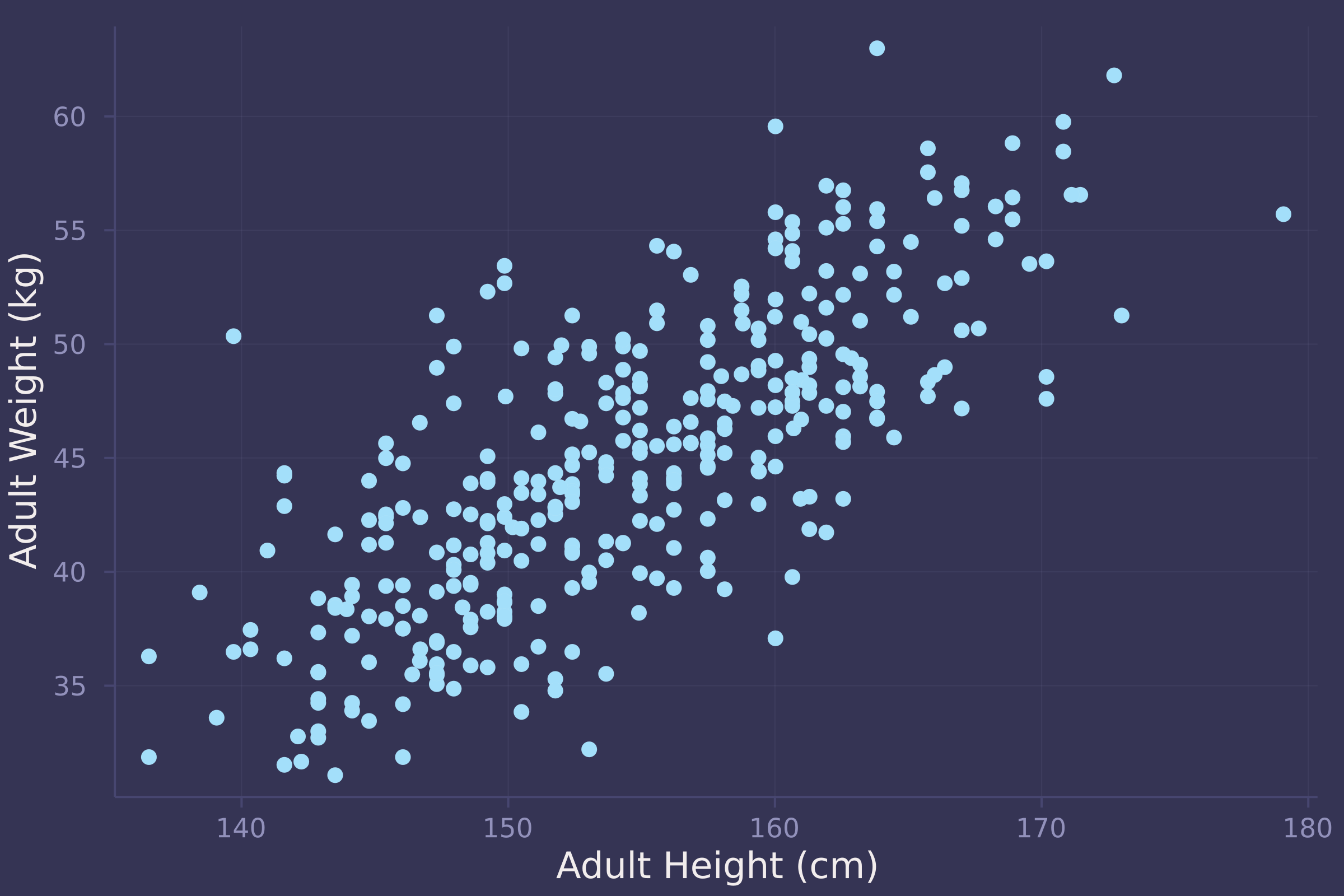
@model function adult_stature(w, h, h̄)
α ~ Normal(50, 10)
β ~ LogNormal(0, 1)
σ ~ Exponential(1)
μ = α .+ β .* (h .- h̄)
w ~ MvNormal(μ, σ)
end;
model = adult_stature(adult.weight, adult.height, mean(adult.height));
post = sample(model, NUTS(), 10_000);
preds = predict(adult_stature(missing, [140, 160, 175], mean(adult.height)), post);
mean(preds) # expected weights
## Mean
## parameters mean
## Symbol Float64
##
## w[1] 35.8370
## w[2] 48.3595
## w[3] 57.7743
quantile(preds, q=[0.055, 0.945]) # 89% intervals
## Quantiles
## parameters 5.5% 94.5%
## Symbol Float64 Float64
##
## w[1] 29.2081 42.6792
## w[2] 41.5726 55.0810
## w[3] 50.9816 64.6083
2. From the Howell1 dataset, consider only the people younger than 13 years old. Estimate the causal association between age and weight. Assume that age influences weight through two paths. First, age influences height, and height influences weight. Second, age directly influences weight through age-related changes in muscle growth and body proportions. All of this implies this causal model (DAG):
Use a linear regression to estimate the total (not just direct) causal effect of each year of growth on weight. Be sure to carefully consider the priors. Try using prior predictive simulation to assess what they imply.
@model function child_stature(w, a)
α ~ Normal(4, 1)
β ~ LogNormal(0, 0.5)
σ ~ Exponential(0.5)
μ = α .+ β .* a
w ~ MvNormal(μ, σ)
end;
child = howell[howell.age .< 13, :];
We assess our priors with prior predictive simulations.
model = child_stature(child.weight, child.age);
prior = sample(model, Prior(), 1_000);
age_seq = collect(0:12);
prior_preds = predict(child_stature(missing, age_seq), prior);
prior_preds = dropdims(prior_preds.value, dims=3)';
plot(repeat(age_seq, size(prior_preds, 2)), vec(prior_preds), ylab="Child Weight (kg)", xlab="Child Age", title="Prior Predictive Simulations", alpha=0.1, seriestype=:scatter, legend=false)
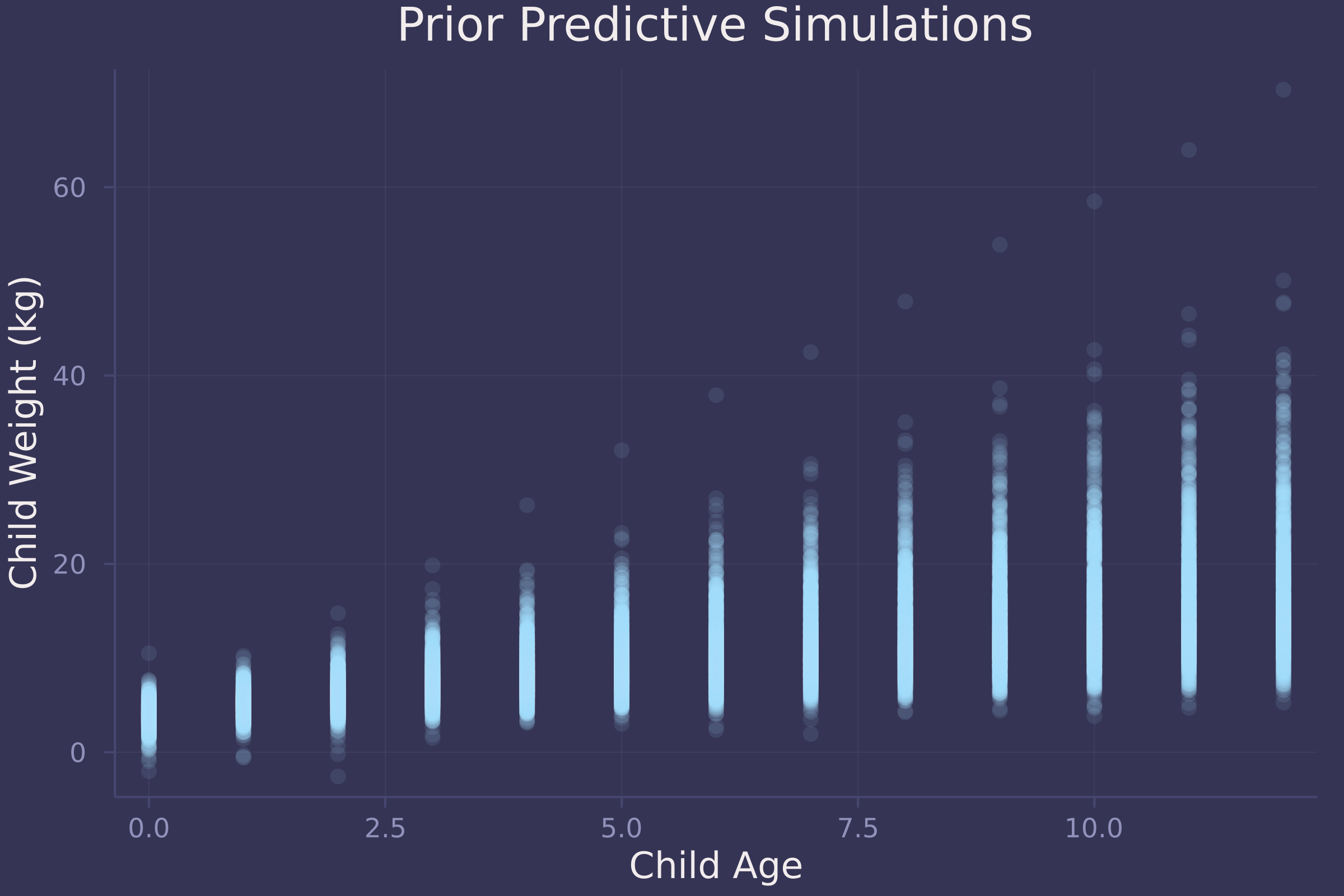
The simulations appear to represent plausible relationships between child age and weight.
What does the data look like?
plot(child.age, child.weight, ylab="Child Weight (kg)", xlab="Child Age", title="Howell's Dobe !Kung Census", seriestype=:scatter, legend=false)
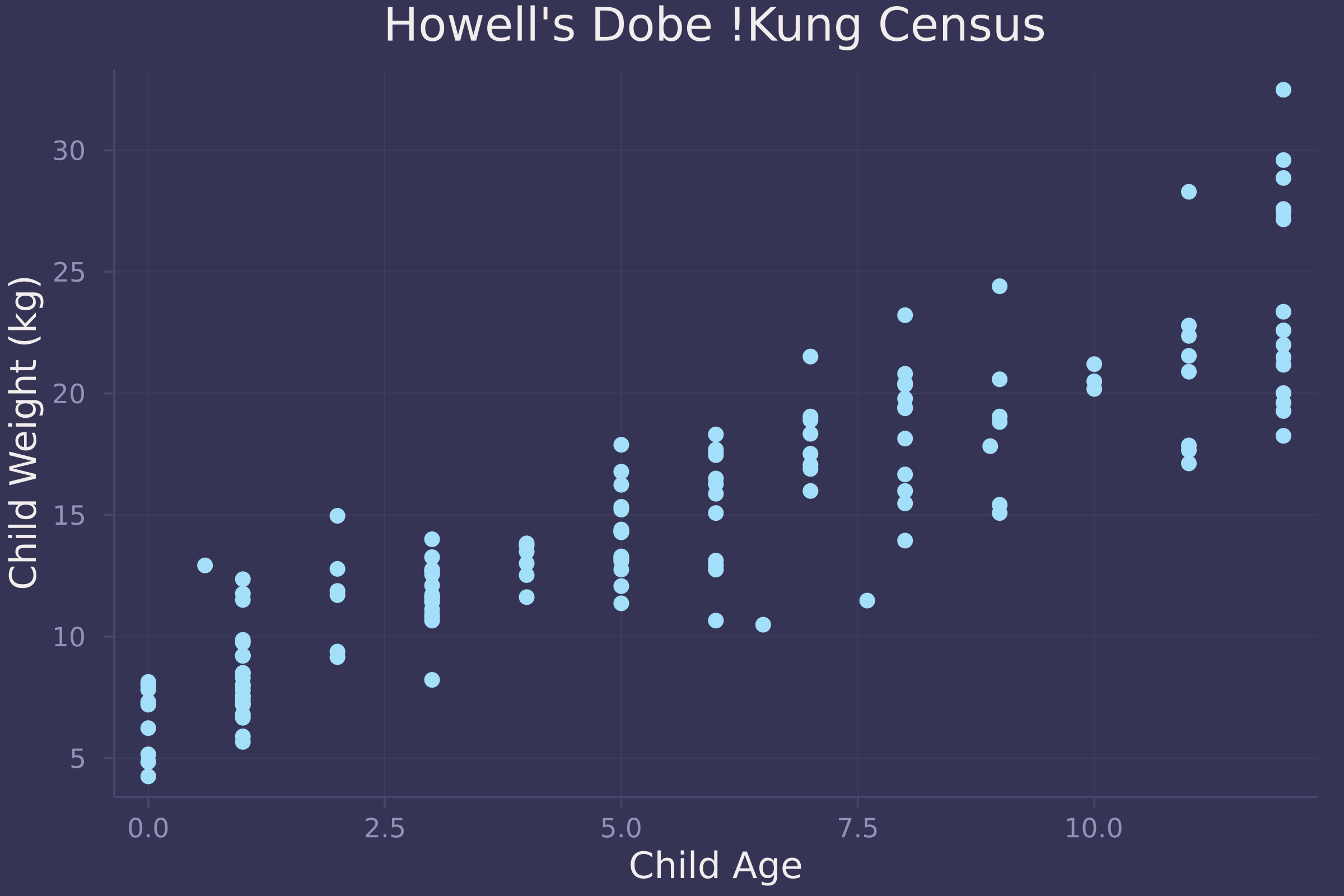
Now we fit a linear regression model to the data and plot the marginal posterior distribution of β, which represents the effect of each year of growth on child weight.
post = sample(model, NUTS(), 10_000)
## Chains MCMC chain (10000×15×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 2.73 seconds
## Compute duration = 2.73 seconds
## parameters = α, β, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α 7.0735 0.3389 0.0034 0.0047 4914.6959 1.0001 ⋯
## β 1.3865 0.0528 0.0005 0.0007 5077.9655 1.0000 ⋯
## σ 2.5251 0.1436 0.0014 0.0019 6465.1057 0.9999 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α 6.4042 6.8446 7.0713 7.3010 7.7484
## β 1.2837 1.3518 1.3863 1.4217 1.4927
## σ 2.2570 2.4268 2.5194 2.6178 2.8275
density(post["β"], ylab="Density", xlab="β", legend=false)
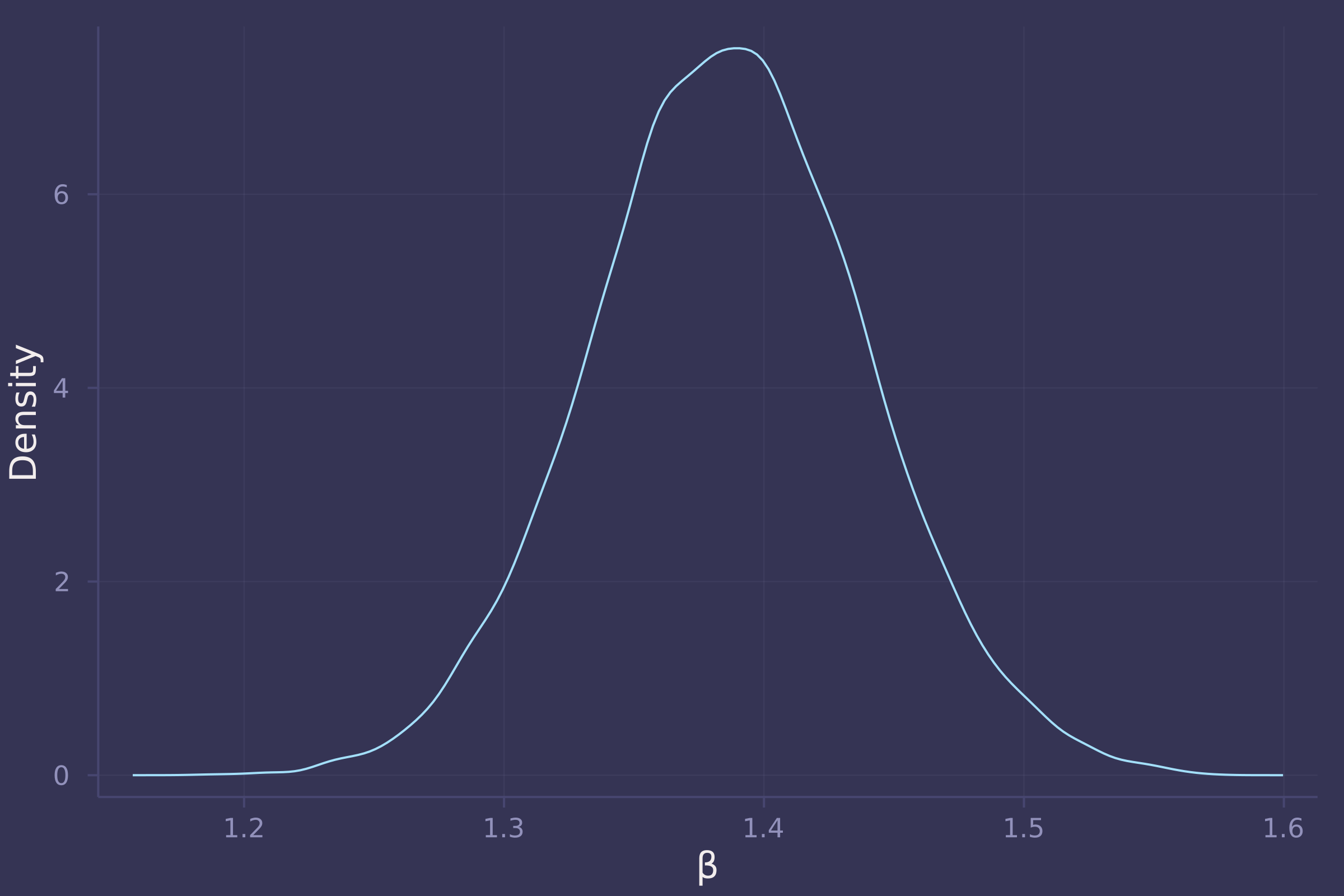
3. Now suppose the causal association between age and weight might be different for boys and girls. Use a single linear regression, with a categorical variable for sex, to estimate the total causal effect of age on weight separately for boys and girls. How do girls and boys differ? Provide one or more posterior contrasts as a summary.
@model function child_stature(w, a, s)
α ~ filldist(Normal(4, 1), 2)
β ~ filldist(LogNormal(0, 0.5), 2)
σ ~ Exponential(0.5)
μ = α[s] .+ β[s] .* a
w ~ MvNormal(μ, σ)
end;
model = child_stature(child.weight, child.age, child.male .+ 1);
post = sample(model, NUTS(), 10_000)
## Chains MCMC chain (10000×17×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 5.19 seconds
## Compute duration = 5.19 seconds
## parameters = α[1], α[2], β[1], β[2], σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α[1] 6.5110 0.4451 0.0045 0.0047 6904.7900 1.0000 ⋯
## α[2] 7.1157 0.4634 0.0046 0.0053 6351.7104 1.0001 ⋯
## β[1] 1.3552 0.0705 0.0007 0.0007 7058.9105 0.9999 ⋯
## β[2] 1.4798 0.0721 0.0007 0.0008 6497.3970 1.0004 ⋯
## σ 2.4642 0.1460 0.0015 0.0016 7756.6571 1.0000 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α[1] 5.6317 6.2189 6.5110 6.8026 7.3883
## α[2] 6.1999 6.7999 7.1251 7.4348 8.0154
## β[1] 1.2166 1.3083 1.3554 1.4020 1.4965
## β[2] 1.3403 1.4305 1.4782 1.5287 1.6224
## σ 2.1978 2.3646 2.4593 2.5545 2.7703
age_seq = range(0, 12, length=50);
w_f = predict(child_stature(missing, age_seq, 1), post);
w_m = predict(child_stature(missing, age_seq, 2), post);
w_diff = dropdims(w_m.value .- w_f.value, dims=3)';
w_diff_mean = vec(mean(w_diff, dims=2));
w_diff_50 = mapslices(x -> quantile(x, [0.25, 0.75]), w_diff, dims=2);
w_diff_70 = mapslices(x -> quantile(x, [0.15, 0.85]), w_diff, dims=2);
w_diff_90 = mapslices(x -> quantile(x, [0.05, 0.95]), w_diff, dims=2);
plot(age_seq, w_diff_mean, ribbon=abs.(w_diff_mean .- w_diff_90), ylab="Male - Female Child Weight Difference (kg)", xlab="Child Age");
plot!(age_seq, w_diff_mean, ribbon=abs.(w_diff_mean .- w_diff_70), legend=false);
plot!(age_seq, w_diff_mean, ribbon=abs.(w_diff_mean .- w_diff_50), legend=false);
plot!(age_seq, fill(0, length(age_seq)), line=:dash, color=:white, legend=false)
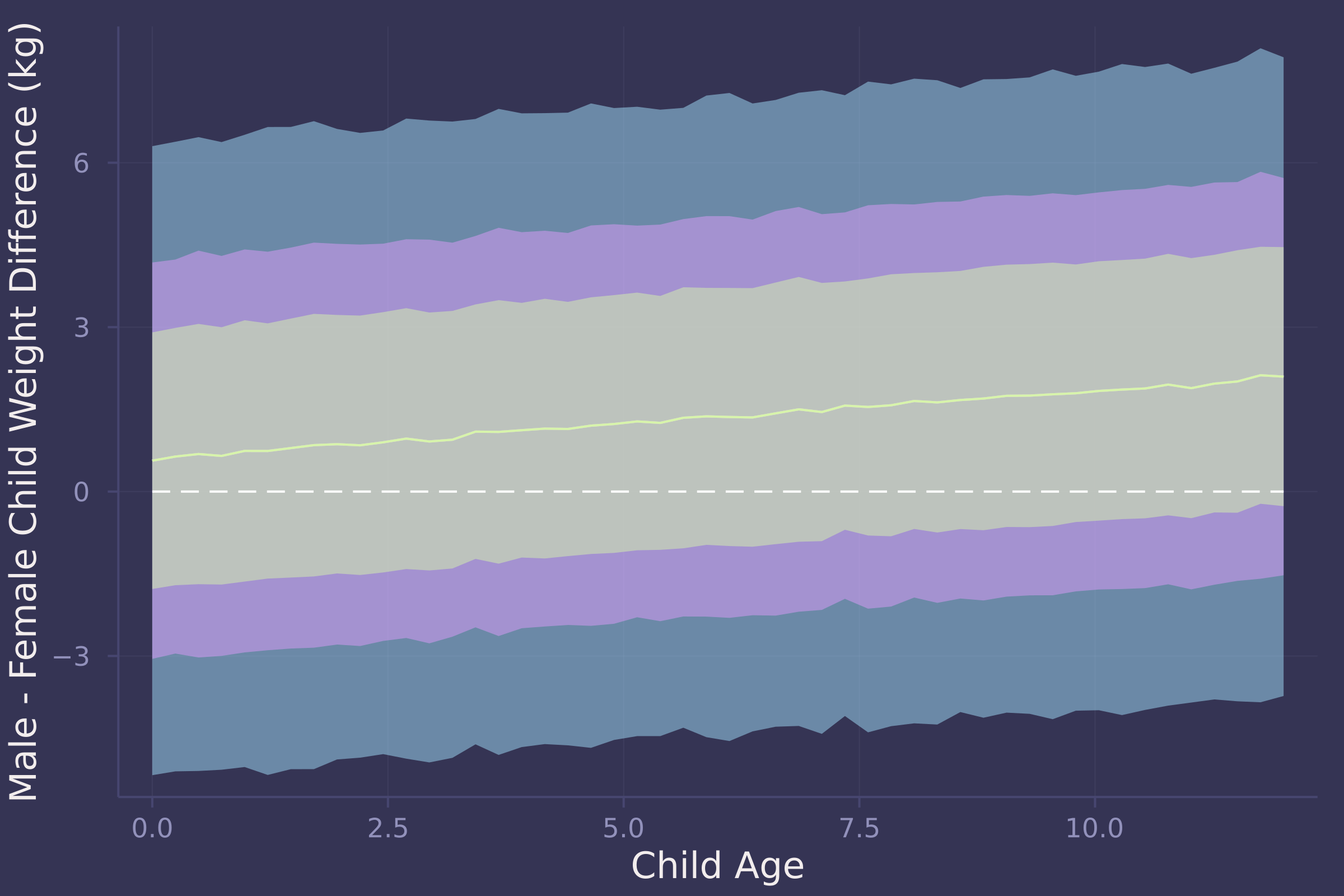
4. OPTIONAL CHALLENGE. The data in oxboys are growth records for 26 boys measured over 9 periods. I want you to model their growth. Specifically, model the increments in growth from one period (Occasion in the data table) to the next. Each increment is simply the difference between height in one occasion and height in the previous occasion. Since none of these boys shrunk during the study, all of the growth increments are greater than zero. Estimate the posterior distribution of these increments. Constrain the distribution so it is always positive — it should not be possible for the model to think that boys can shrink from year to year. Finally compute the posterior distribution of the total growth over all 9 occasions.
oxboys = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/Oxboys.csv"),
DataFrame,
delim=';'
);
oxboys = combine(groupby(oxboys, :Subject), :height => diff => :diff);
oxboys = transform(groupby(oxboys, :Subject), :Subject => (x -> 1:length(x)) => :time)
## 208×3 DataFrame
## Row │ Subject diff time
## │ Int64 Float64 Int64
## ─────┼─────────────────────────
## 1 │ 1 2.9 1
## 2 │ 1 1.4 2
## 3 │ 1 2.3 3
## 4 │ 1 0.6 4
## 5 │ 1 2.5 5
## 6 │ 1 1.5 6
## 7 │ 1 1.6 7
## 8 │ 1 2.5 8
## ⋮ │ ⋮ ⋮ ⋮
## 202 │ 26 0.8 2
## 203 │ 26 1.6 3
## 204 │ 26 1.7 4
## 205 │ 26 0.5 5
## 206 │ 26 2.9 6
## 207 │ 26 0.8 7
## 208 │ 26 0.5 8
## 193 rows omitted
@model function oxboy_growth(d, t)
μ ~ filldist(Normal(0, 0.2), length(unique(t)))
σ ~ Exponential(0.2)
d ~ MvLogNormal(μ[t], σ)
end;
prior = sample(oxboy_growth(oxboys.diff, oxboys.time), Prior(), 1_000);
prior_preds = predict(oxboy_growth(missing, 1:8), prior);
prior_preds = dropdims(prior_preds.value, dims=3)';
plot(repeat(1:8, size(prior_preds, 2)), vec(prior_preds), ylab="Height increment (cm)", xlab="Time", title="Prior Predictive Simulations", alpha=0.1, seriestype=:scatter, legend=false)
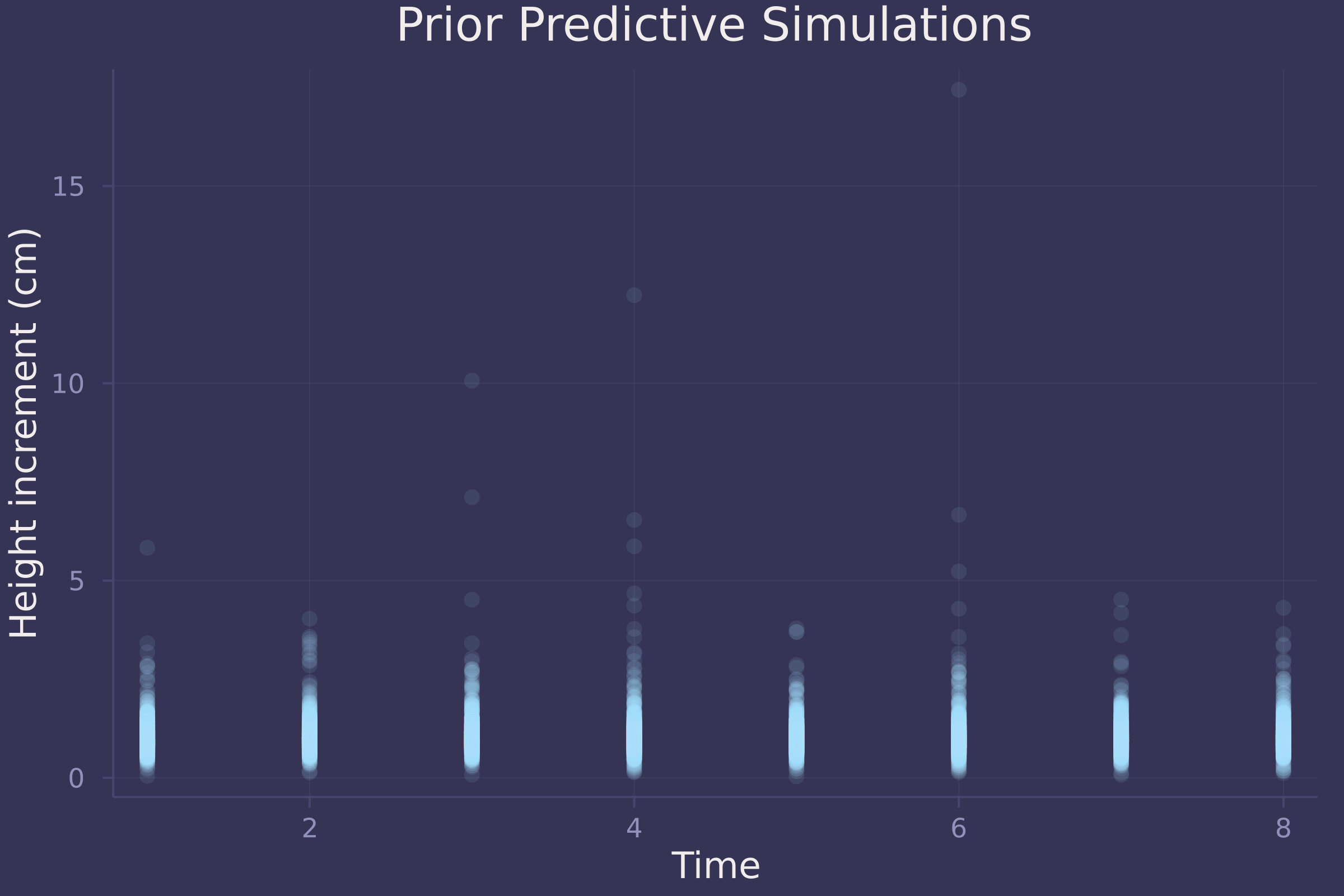
Not great prior predictive simulations. A downside to using the Log-Normal distribution here is that it produces skewed, unrealistically high height increments.
Let’s take a look at the actual data.
plot(oxboys.time, oxboys.diff, ylab="Height increment (cm)", xlab="Time", seriestype=:scatter, legend=false)
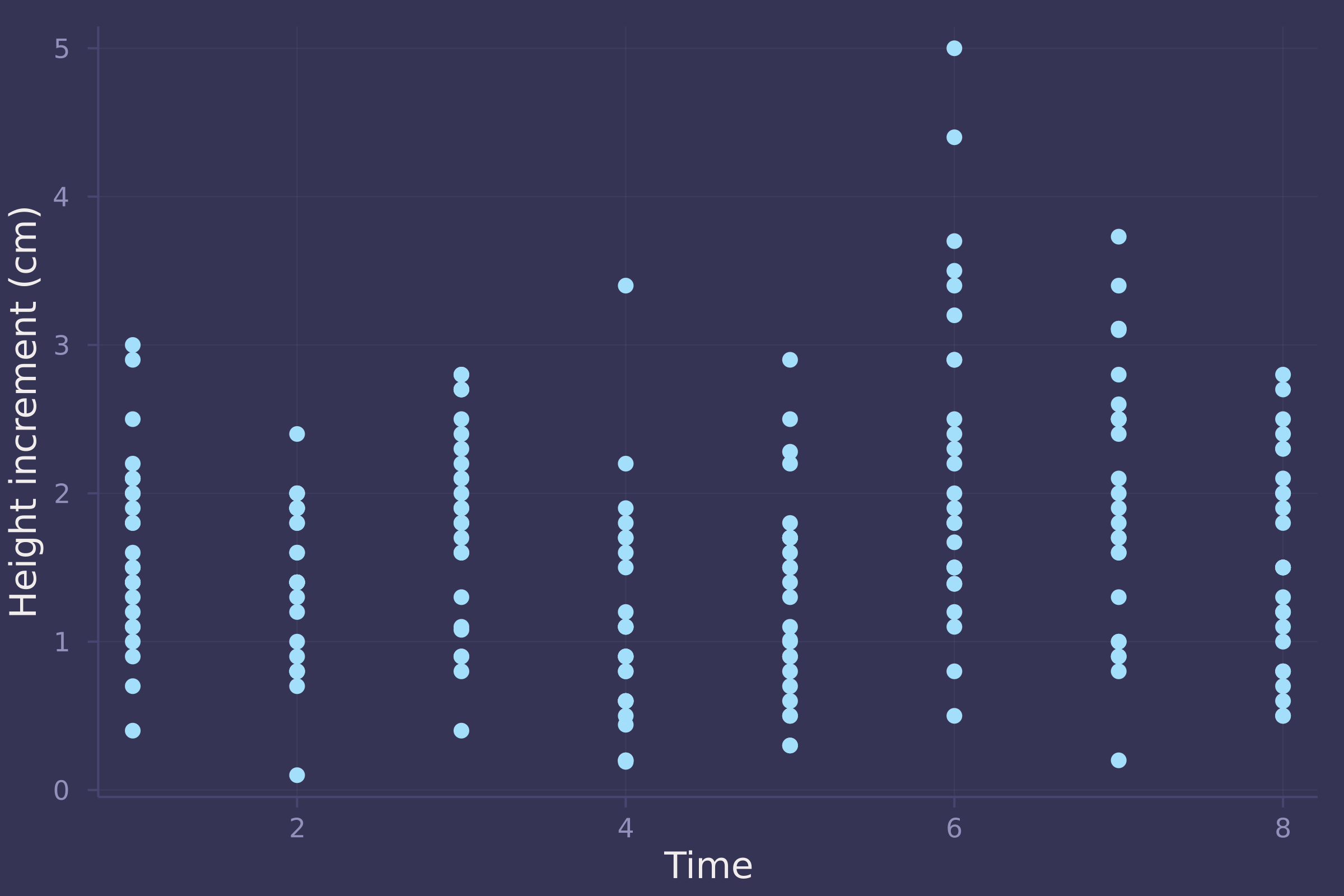
model = oxboy_growth(oxboys.diff, oxboys.time);
post = sample(model, MH(), 10_000)
## Chains MCMC chain (10000×10×1 Array{Float64, 3}):
##
## Iterations = 1:1:10000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 1.27 seconds
## Compute duration = 1.27 seconds
## parameters = μ[1], μ[2], μ[3], μ[4], μ[5], μ[6], μ[7], μ[8], σ
## internals = lp
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat es ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## μ[1] 0.1066 0.0640 0.0006 0.0060 28.6541 1.1949 ⋯
## μ[2] 0.0383 0.1057 0.0011 0.0103 24.9660 1.0002 ⋯
## μ[3] 0.3841 0.1318 0.0013 0.0129 25.4927 1.1567 ⋯
## μ[4] 0.0904 0.1118 0.0011 0.0108 26.1662 1.0012 ⋯
## μ[5] -0.0287 0.1563 0.0016 0.0153 21.6931 2.3444 ⋯
## μ[6] 0.3885 0.1773 0.0018 0.0176 22.2689 1.7977 ⋯
## μ[7] 0.1270 0.1957 0.0020 0.0192 21.8922 2.1461 ⋯
## μ[8] 0.0392 0.1565 0.0016 0.0149 26.0338 1.2843 ⋯
## σ 0.6287 0.0303 0.0003 0.0028 34.1437 1.0116 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## μ[1] -0.0525 0.0540 0.1406 0.1406 0.2141
## μ[2] -0.1046 -0.0178 0.0321 0.0321 0.3453
## μ[3] -0.0298 0.3492 0.3760 0.4851 0.4851
## μ[4] -0.1932 0.1032 0.1032 0.1926 0.1926
## μ[5] -0.1766 -0.1766 -0.0400 0.0496 0.2723
## μ[6] -0.0027 0.2869 0.2869 0.5695 0.5695
## μ[7] -0.0537 -0.0537 0.0118 0.3640 0.3982
## μ[8] -0.1523 -0.1523 0.1228 0.1228 0.3487
## σ 0.5276 0.6318 0.6318 0.6446 0.6446
d_sim = predict(oxboy_growth(missing, 1:8), post);
d_sim = dropdims(d_sim.value, dims=3)';
d_mean = vec(mean(d_sim, dims=2));
d_90 = mapslices(x -> quantile(x, [0.05, 0.95]), d_sim, dims=2);
plot(oxboys.time, oxboys.diff, ylab="Height increment (cm)", xlab="Time", seriestype=:scatter, alpha=0.3, legend=false);
plot!(1:8, d_mean, seriestype=:scatter, yerror=(d_mean .- d_90), markersize=8, legend=false)
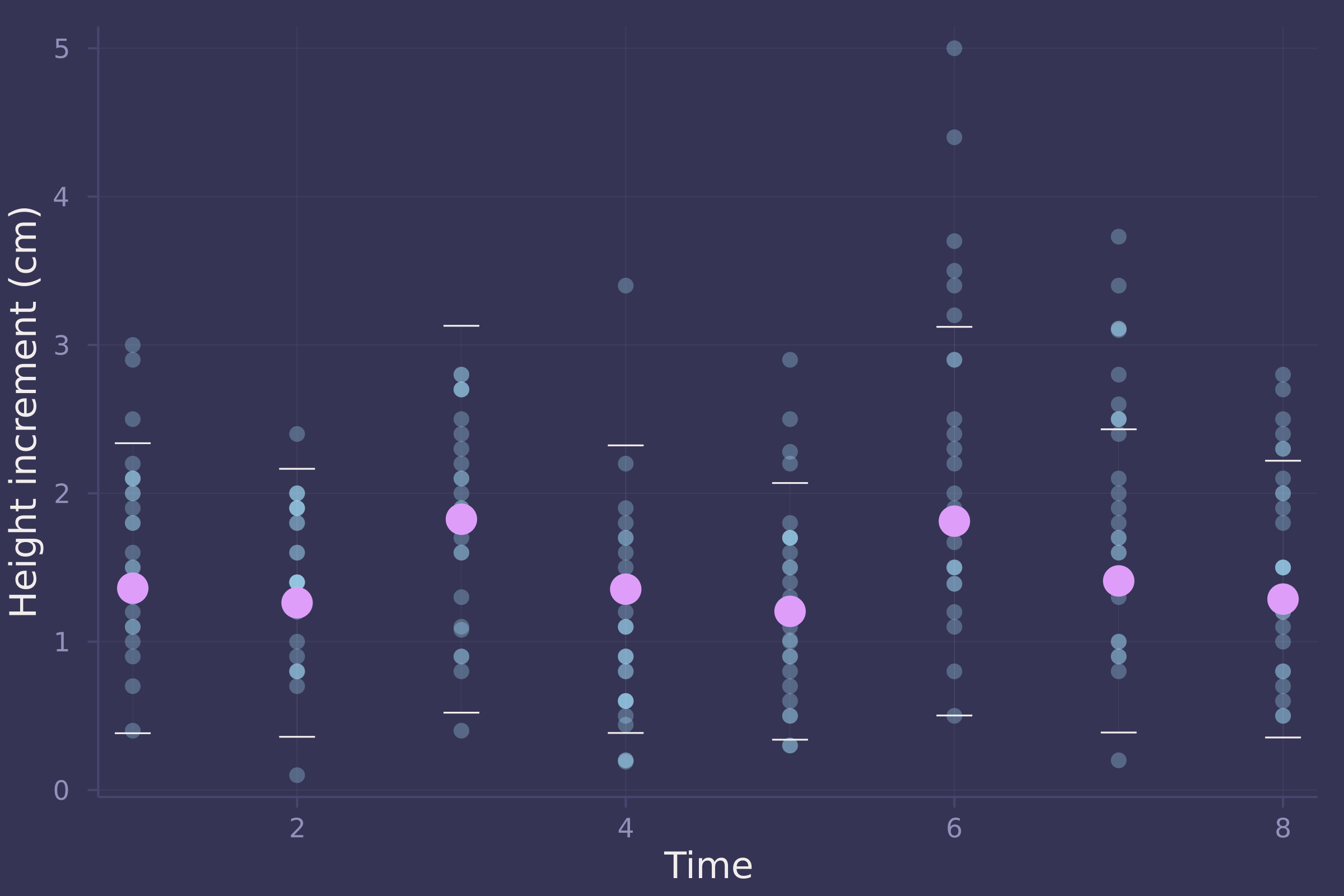
growth_sim = vec(sum(d_sim, dims=1));
density(growth_sim, ylab="Density", xlab="Total growth (cm)", legend=false)
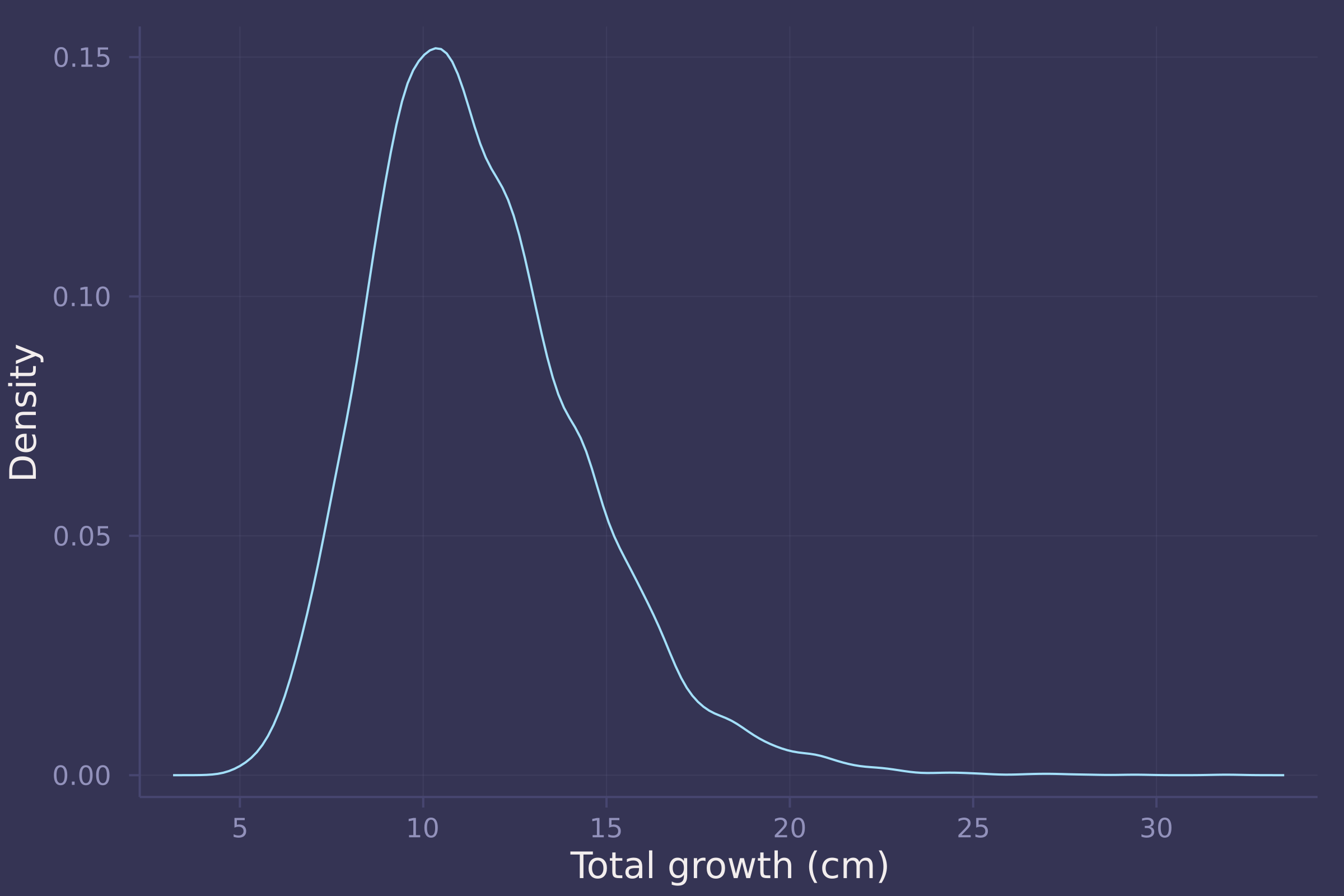
Homework 3
1. The first two problems are based on the same data. The data in foxes are 116 foxes from 30 different urban groups in England. These fox groups are like street gangs. Group size (groupsize) varies from 2 to 8 individuals. Each group maintains its own (almost exclusive) urban territory. Some territories are larger than others. The area variable encodes this information. Some territories also have more avgfood than others. And food influences the weight of each fox. Assume this DAG:
where F is avgfood, G is groupsize, A is area, and W is weight.
Use the backdoor criterion and estimate the total causal influence of A on F . What effect would increasing the area of a territory have on the amount of food inside it?
foxes = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/foxes.csv"),
DataFrame,
delim=';'
)
## 116×5 DataFrame
## Row │ group avgfood groupsize area weight
## │ Int64 Float64 Int64 Float64 Float64
## ─────┼─────────────────────────────────────────────
## 1 │ 1 0.37 2 1.09 5.02
## 2 │ 1 0.37 2 1.09 2.84
## 3 │ 2 0.53 2 2.05 5.33
## 4 │ 2 0.53 2 2.05 6.07
## 5 │ 3 0.49 2 2.12 5.85
## 6 │ 3 0.49 2 2.12 3.25
## 7 │ 4 0.45 2 1.29 4.53
## 8 │ 4 0.45 2 1.29 4.09
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮
## 110 │ 29 0.67 4 2.75 5.0
## 111 │ 29 0.67 4 2.75 3.81
## 112 │ 29 0.67 4 2.75 4.81
## 113 │ 29 0.67 4 2.75 3.94
## 114 │ 30 0.41 3 1.91 3.16
## 115 │ 30 0.41 3 1.91 2.78
## 116 │ 30 0.41 3 1.91 3.86
## 101 rows omitted
@model function fox_area_on_food_total(f, a)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* a
f ~ MvNormal(μ, σ)
end;
standardize(x) = (x .- mean(x)) ./ std(x);
model = fox_area_on_food_total(
standardize(foxes.avgfood),
standardize(foxes.area)
);
post = sample(model, NUTS(), 10_000)
## Chains MCMC chain (10000×15×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 3.27 seconds
## Compute duration = 3.27 seconds
## parameters = α, β, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α -0.0006 0.0430 0.0004 0.0004 14291.7230 0.9999 ⋯
## β 0.8762 0.0437 0.0004 0.0004 14647.8061 0.9999 ⋯
## σ 0.4757 0.0323 0.0003 0.0003 14247.4144 1.0000 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α -0.0855 -0.0291 -0.0009 0.0278 0.0844
## β 0.7889 0.8472 0.8763 0.9053 0.9627
## σ 0.4172 0.4531 0.4739 0.4964 0.5447
area_seq = range(-2, 2, length=50);
f_preds = predict(fox_area_on_food_total(missing, area_seq), post);
f_preds = dropdims(f_preds.value, dims=3)';
f_preds_mean = vec(mean(f_preds, dims=2));
f_preds_50 = mapslices(x -> quantile(x, [0.25, 0.75]), f_preds, dims=2);
f_preds_70 = mapslices(x -> quantile(x, [0.15, 0.85]), f_preds, dims=2);
f_preds_90 = mapslices(x -> quantile(x, [0.05, 0.95]), f_preds, dims=2);
plot(area_seq, f_preds_mean, ribbon=abs.(f_preds_mean .- f_preds_90), ylab="Average Food (Standardized)", xlab="Area (Standardized)", legend=false);
plot!(area_seq, f_preds_mean, ribbon=abs.(f_preds_mean .- f_preds_70), legend=false);
plot!(area_seq, f_preds_mean, ribbon=abs.(f_preds_mean .- f_preds_50), legend=false)
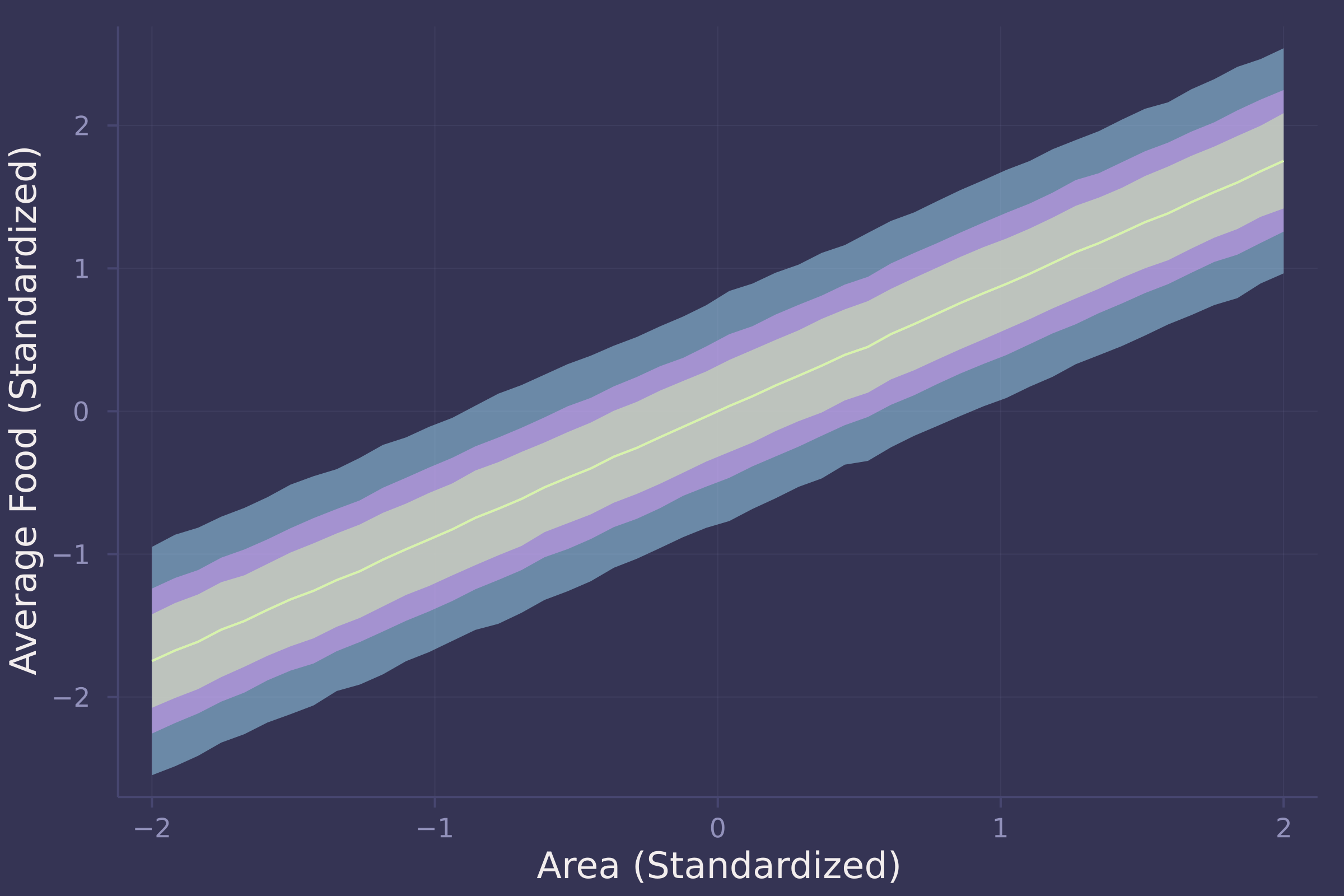
There is a strong positive relationship between area and food — the larger an area, the more food available within it.
2. Now infer both the total and direct causal effects of adding food F to a territory on the weight W of foxes. Which covariates do you need to adjust for in each case? In light of your estimates from this problem and the previous one, what do you think is going on with these foxes? Feel free to speculate — all that matters is that you justify your speculation.
To answer this we will fit two models, one that captures the total causal effect of food on weight, and another that captures the direct causal effect of food on weight.
For the total model, we simply regress weight on food.
@model function fox_food_on_weight_total(w, f)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* f
w ~ MvNormal(μ, σ)
end;
model_total = fox_food_on_weight_total(
standardize(foxes.weight),
standardize(foxes.avgfood)
);
post_total = sample(model_total, NUTS(), 10_000)
## Chains MCMC chain (10000×15×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 2.31 seconds
## Compute duration = 2.31 seconds
## parameters = α, β, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α -0.0014 0.0845 0.0008 0.0007 15177.4868 0.9999 ⋯
## β -0.0240 0.0924 0.0009 0.0008 15388.6857 0.9999 ⋯
## σ 1.0088 0.0659 0.0007 0.0006 14648.4465 0.9999 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α -0.1666 -0.0576 -0.0005 0.0551 0.1629
## β -0.2055 -0.0861 -0.0244 0.0366 0.1573
## σ 0.8883 0.9630 1.0060 1.0516 1.1458
density(post_total[:β], ylab="Density", xlab="Parameter Value", label="β")
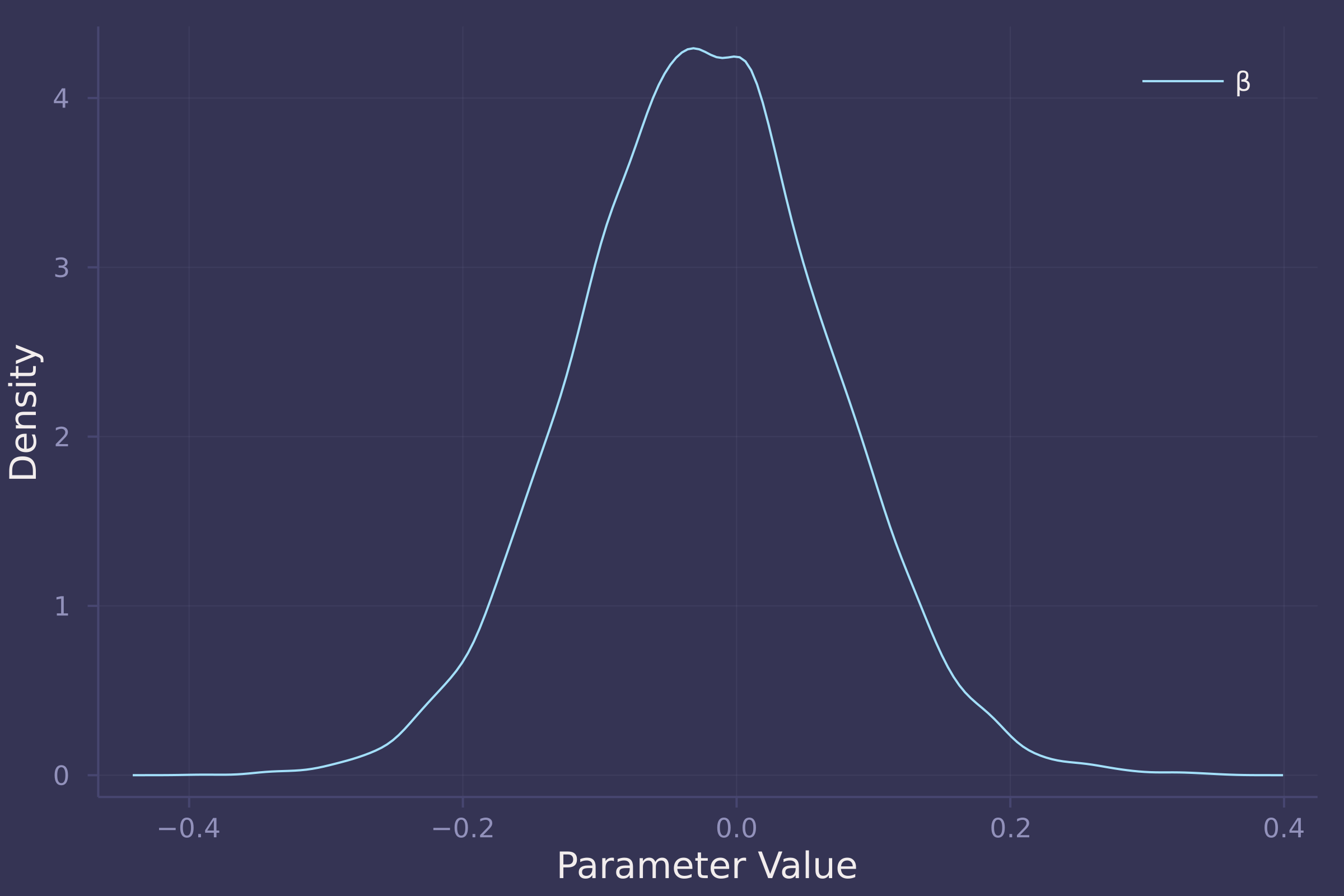
The total effect of food on weight appears negligible. In the total model, β (coefficient of food) is estimated to be approximately centered at zero with an equal spread of both positive and negative values.
Now for the direct model, we regress weight on food and group size, a mediator of food and weight.
@model function fox_food_on_weight_direct(w, f, g)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
γ ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* f .+ γ .* g
w ~ MvNormal(μ, σ)
end;
model_direct = fox_food_on_weight_direct(
standardize(foxes.weight),
standardize(foxes.avgfood),
standardize(foxes.groupsize)
);
post_direct = sample(model_direct, NUTS(), 10_000)
## Chains MCMC chain (10000×16×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 4.84 seconds
## Compute duration = 4.84 seconds
## parameters = α, β, γ, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α 0.0016 0.0815 0.0008 0.0008 9342.7736 1.0000 ⋯
## β 0.4727 0.1827 0.0018 0.0022 6287.6286 1.0000 ⋯
## γ -0.5682 0.1827 0.0018 0.0022 6440.0546 1.0002 ⋯
## σ 0.9621 0.0626 0.0006 0.0006 9208.1096 1.0003 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α -0.1606 -0.0518 0.0012 0.0546 0.1624
## β 0.1087 0.3528 0.4728 0.5950 0.8263
## γ -0.9222 -0.6931 -0.5714 -0.4460 -0.2011
## σ 0.8475 0.9178 0.9594 1.0027 1.0924
density([post_direct[:β], post_direct[:γ]], ylab="Density", xlab="Parameter Value", label=["β" "γ"])
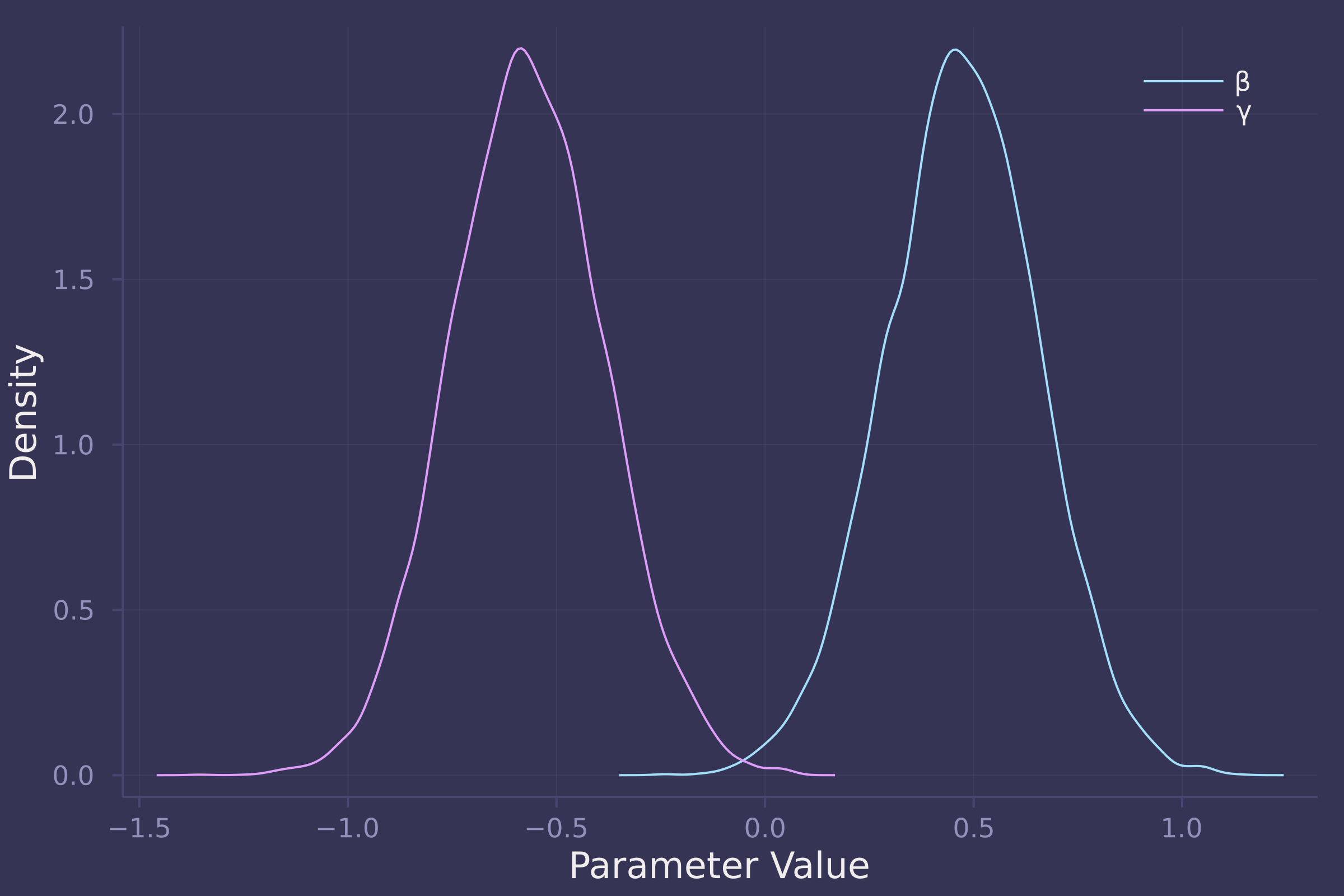
Unlike the total effect, the direct effect of food on weight is reliably positive in a model that also contains group size, which is reliably negative of an almost equal magnitude. In the direct model, β (coefficient of food) is estimated to be centered at 0.5 with most of its density between 0 and 1, while γ (coefficient of group size) is estimated to be centered at -0.6 with most of its density between -1 and 0.
Taken together, the model results suggest that the effect of food on a fox’s weight is almost entirely offset by group size. Put another way, more food available in an urban territory leads to an increase in the number of foxes within that territory, preventing any potential increase in a fox’s weight due to available food.
3. Reconsider the Table 2 Fallacy (from Lecture 6), this time with an unobserved confound U that influences both smoking S and stroke Y . Here’s the modified DAG:
First use the backdoor criterion to determine the adjustment set that allows you to estimate the causal effect of_ X on Y , i.e. P(Y ∣ do(X)) . Second explain the proper interpretation of each coefficient implied by the regression model that corresponds to the adjustment set. Which coefficients (slopes) are causal and which are not? There is not need to fit any models. Just think through the implications.
Alright, no code required for this problem. Let’s think through everything logically.
The backdoor criterion says we need to block any paths that connect X and Y that enter X from the backdoor. There are two such paths.
The first path is X ← A → Y . Here, A is a confounder of X and Y . To block the path, we include A in our adjustment set.
The second path is X ← S → Y . S too is a confounder of X and Y so we also include S in our adjustment set to the block path.
Now, with the adjustment set {A, S} we can properly estimate the causal effect of X on Y . Great! So what’s the problem?
The unobserved variable U wreaks havoc on the other coefficients in the model, contributing to a Table 2 Fallacy.
Take the variable A . As we have conditioned on A and S , and S is a collider of A and U , our estimate of the effect of A on Y in our model is biased by U .
Similarly, U is a confounder of S and Y , biasing the estimate of the effect of S on Y as well.
The takeaway here is that even with an adjustment set that allows us to properly estimate the causal effect of X on Y , we are not guaranteed unbiased estimates of other coefficients in the model which may be polluted by unobserved variables we are unable to control for.
4. OPTIONAL CHALLENGE. Write a synthetic data simulation for the causal model shown in Problem 3. Be sure to include the unobserved confound in the simulation. Choose any functional relationships that you like — you don’t have to get the epidemiology correct. You just need to honor the causal structure. Then design a regression model to estimate the influence of X on Y and use it on your synthetic data. How lrge of a sample do you need to reliably estimate P(Y ∣ do(X)) ? Define “reliably” as you like, but justify your definition.
First, we define a function to generate synthetic data. As the DAG in Problem 3 models the risk of stroke, represented by Y , we call the function generate_strokes() (at the risk of sounding like a diabolical supervillain).
function generate_strokes(n; β = 1)
a = randn(n)
u = randn(n)
s = rand.(Normal.(a .+ u))
x = rand.(Normal.(a .+ s))
y = rand.(Normal.(a .+ s .+ u .+ β .* x))
DataFrame(:x => x, :y => y, :a => a, :s => s)
end;
We’ll also define a regression model called model_strokes().
@model function model_strokes(y, x, a, s)
α ~ Normal(0, 1)
β ~ Normal(0, 1)
γ ~ Normal(0, 1)
δ ~ Normal(0, 1)
σ ~ Exponential(1)
μ = α .+ β .* x .+ γ .* a .+ δ .* s
y ~ MvNormal(μ, σ)
end;
And finally a simulation function called simulate_strokes() which generates a dataset given a sample size n, fits a model, samples from the posterior, and makes a density plot of β which it adds to an existing base plot p.
function simulate_strokes!(p, n)
strokes = generate_strokes(n)
model = model_strokes(strokes.y, strokes.x, strokes.a, strokes.s)
post = sample(model, NUTS(), 10_000)
density!(p, post[:β])
end;
Now let’s investigate the accuracy of our estimate of β under three sample sizes: 10, 100, and 1,000.
using Random
Random.seed!(42);
p = plot([1, 1], [0, 12], ylab="Density", xlab="β", xlims=[-1, 3], line=:dash, color=:white, legend=false);
p10 = deepcopy(p);
p100 = deepcopy(p);
p1000 = deepcopy(p);
for _ in 1:5
simulate_strokes!(p10, 10);
simulate_strokes!(p100, 100);
simulate_strokes!(p1000, 1000);
end;
plot!(p10, title="n = 10")
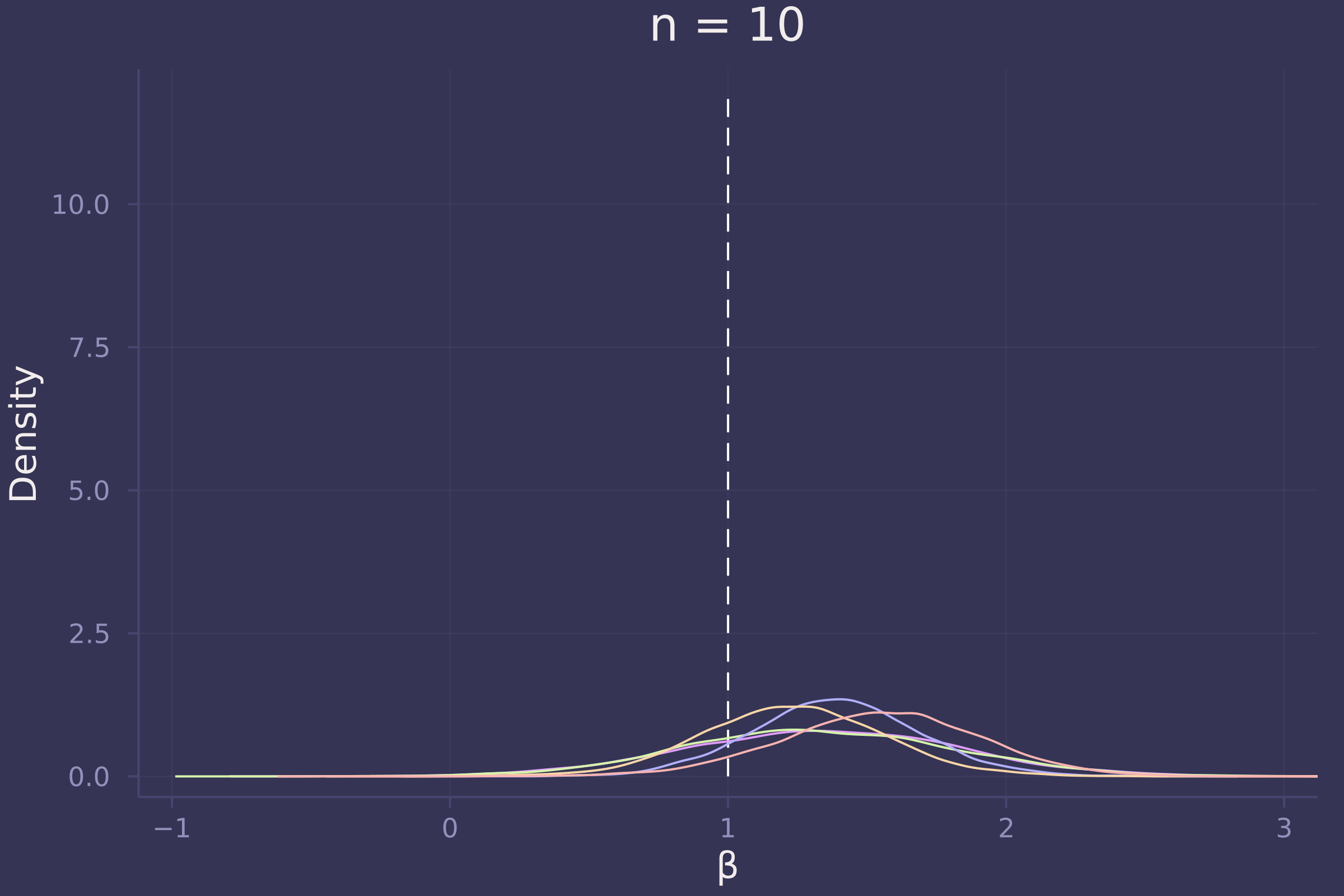
plot!(p100, title="n = 100")
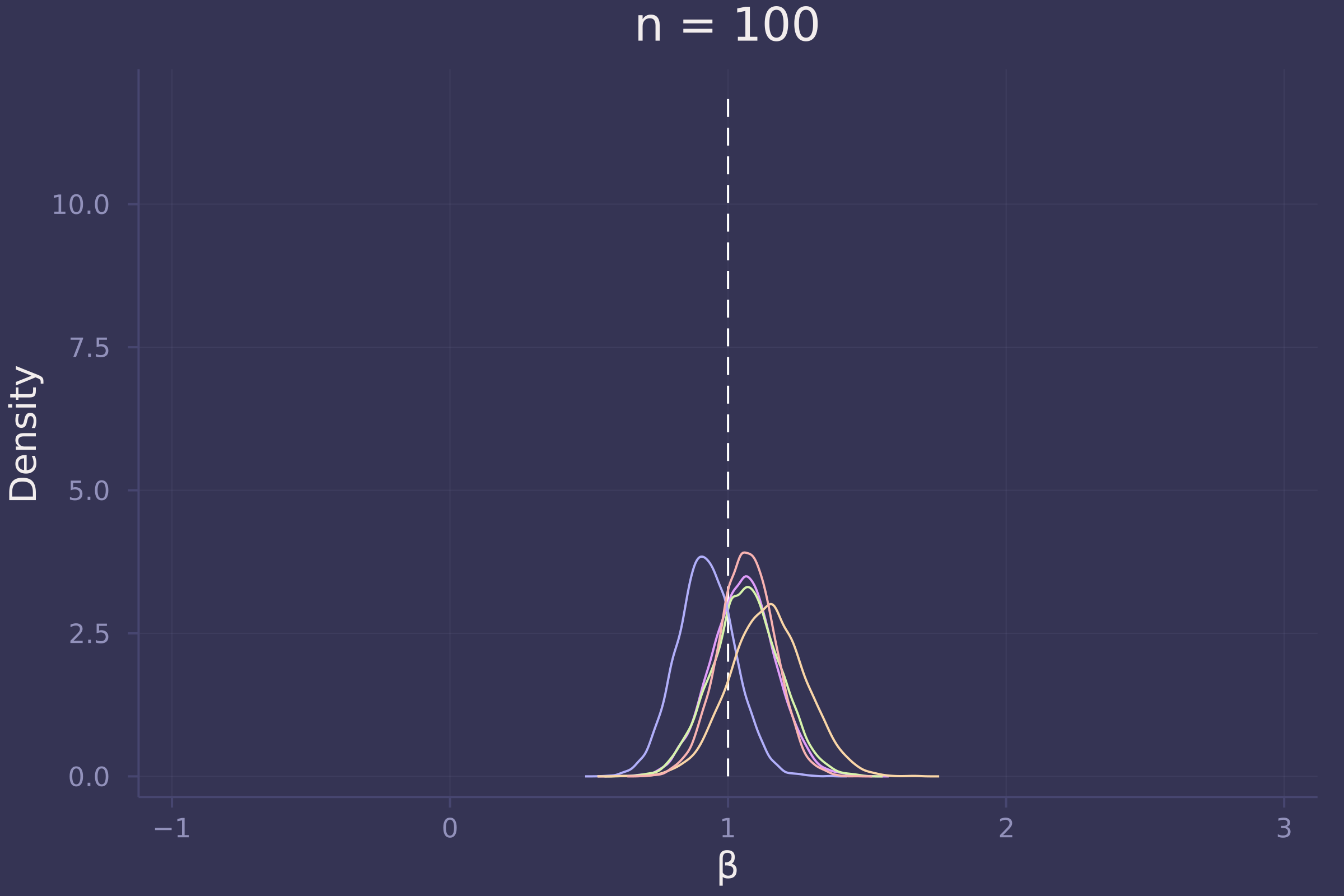
plot!(p1000, title="n = 1000")
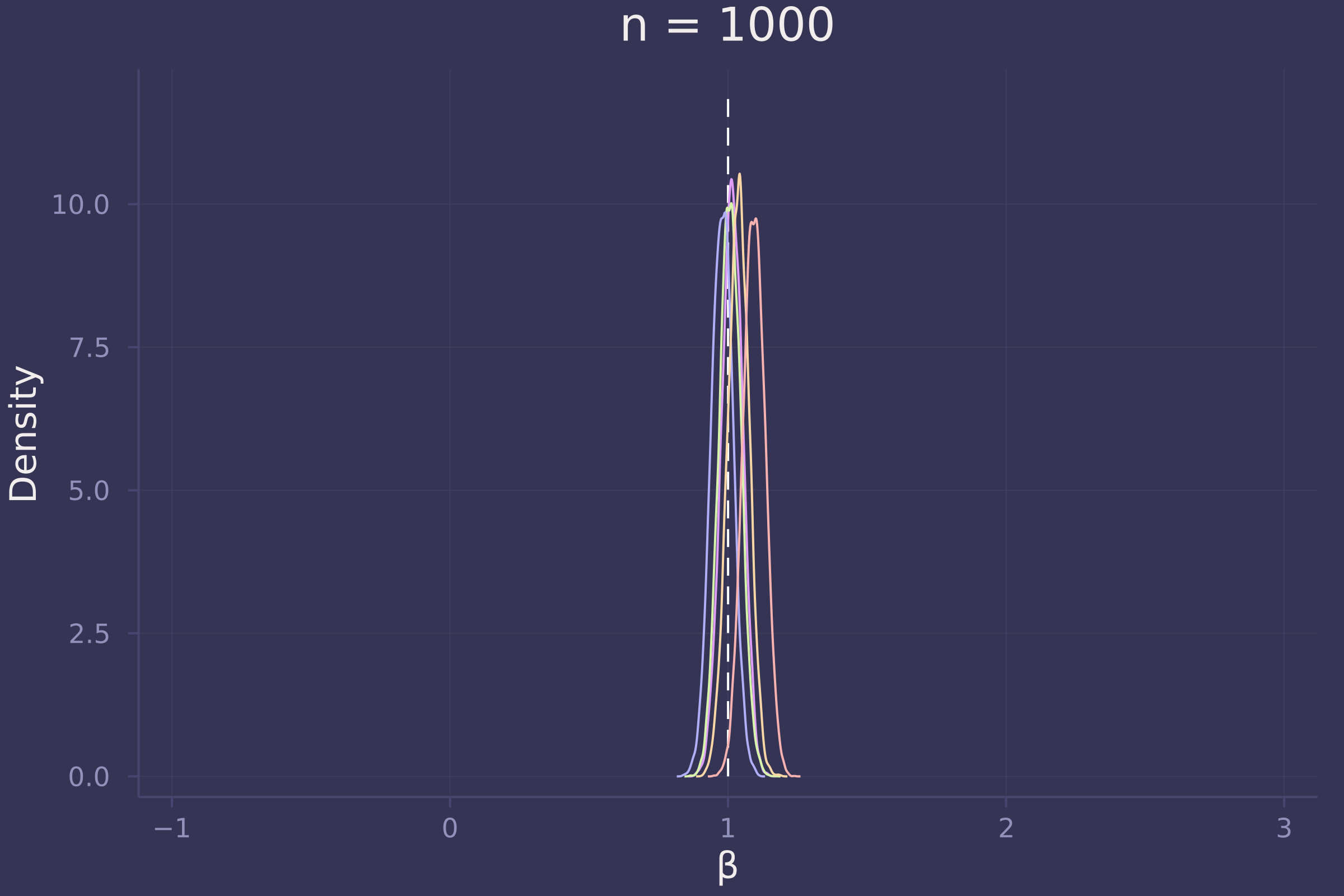
Foregoing a formal definition of “reliable” (as the question insists), it appears as though the estimates of β become reliable-ish with a sample size approaching 100.
Homework 4
1. Revisit the marriage, age, and happiness collider bias example from Chapter 6. Run models m6.9 and m6.10 (pages 178-179). Compare these two models using PSIS and WAIC. Which model is expected to make better predictions, according to these criteria? On the basis of the causal model, how should you interpret the parameter estimates from the model preferred by PSIS and WAIC?
function generate_persons(; n_years=1000, max_age=65, n_births=20, age_of_marriage=18)
# https://github.com/rmcelreath/rethinking/blob/master/R/sim_happiness.R
invlogit(x) = 1 ./ (exp(-x) .+ 1)
age = fill(1, n_births)
married = fill(false, n_births)
happiness = collect(range(-2, 2, length=n_births))
for _ in 1:n_years
age .+= 1
append!(age, fill(1, n_births))
append!(married, fill(false, n_births))
append!(happiness, collect(range(-2, 2, length=n_births)))
for i in eachindex(age, married, happiness)
if age[i] >= age_of_marriage && !married[i]
married[i] = rand(Bernoulli(invlogit(happiness[i] - 4)))
end
end
deaths = findall(age .> max_age)
deleteat!(age, deaths)
deleteat!(married, deaths)
deleteat!(happiness, deaths)
end
DataFrame(
age = age,
married = convert.(Int, married),
happiness = happiness
)
end;
persons = generate_persons();
adults = persons[persons.age .> 17, :];
min_age, max_age = extrema(adults.age);
adults.age = (adults.age .- min_age) ./ (max_age - min_age);
@model function with_collider(h, a, m)
α ~ filldist(Normal(0, 1), 2)
β ~ Normal(0, 2)
σ ~ Exponential(1)
μ = α[m] .+ β .* a
h .~ Normal.(μ, σ)
end;
model_with_collider = with_collider(
adults.happiness,
adults.age,
adults.married .+ 1
);
post_with_collider = sample(model_with_collider, NUTS(), 10_000)
## Chains MCMC chain (10000×16×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 16.23 seconds
## Compute duration = 16.23 seconds
## parameters = α[1], α[2], β, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α[1] -0.2066 0.0641 0.0006 0.0009 5215.8579 1.0000 ⋯
## α[2] 1.2387 0.0879 0.0009 0.0013 4748.6592 1.0003 ⋯
## β -0.7526 0.1150 0.0011 0.0017 4351.4088 0.9999 ⋯
## σ 1.0109 0.0233 0.0002 0.0003 7107.2851 1.0000 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α[1] -0.3321 -0.2498 -0.2072 -0.1634 -0.0791
## α[2] 1.0675 1.1796 1.2387 1.2964 1.4118
## β -0.9782 -0.8299 -0.7523 -0.6766 -0.5229
## σ 0.9662 0.9952 1.0103 1.0261 1.0586
@model function without_collider(h, a)
α ~ Normal(0, 1)
β ~ Normal(0, 2)
σ ~ Exponential(1)
μ = α .+ β .* a
h .~ Normal.(μ, σ)
end;
model_without_collider = without_collider(
adults.happiness,
adults.age
);
post_without_collider = sample(model_without_collider, NUTS(), 10_000)
## Chains MCMC chain (10000×15×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 7.74 seconds
## Compute duration = 7.74 seconds
## parameters = α, β, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α -0.0003 0.0772 0.0008 0.0011 4709.7550 0.9999 ⋯
## β 0.0004 0.1337 0.0013 0.0020 4485.6562 0.9999 ⋯
## σ 1.2160 0.0280 0.0003 0.0004 6816.9221 0.9999 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α -0.1505 -0.0518 0.0004 0.0510 0.1525
## β -0.2633 -0.0914 0.0000 0.0887 0.2645
## σ 1.1630 1.1968 1.2151 1.2347 1.2731
psis_loo(model_with_collider, post_with_collider, source=:mcmc)
# -1360
psis_loo(model_without_collider, post_without_collider, source=:mcmc)
# -1551
2. Reconsider the urban fox analysis from Homework 3. On the basis of PSIS and WAIC scores, which combination of variables best predicts body weight ( W , weight)? How would you interpret the estimates from the best scoring model?
foxes.area = standardize(foxes.area);
foxes.avgfood = standardize(foxes.avgfood);
foxes.groupsize = standardize(foxes.groupsize);
foxes.weight = standardize(foxes.weight);
@model function fox1(w, x)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* x
w .~ Normal.(μ, σ)
end;
@model function fox2(w, x, y)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
γ ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* x .+ γ .* y
w .~ Normal.(μ, σ)
end;
@model function fox3(w, x, y, z)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
γ ~ Normal(0, 0.5)
δ ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* x .+ γ .* y .+ δ .* z
w .~ Normal.(μ, σ)
end;
model_f = fox1(foxes.weight, foxes.avgfood);
model_g = fox1(foxes.weight, foxes.groupsize);
model_fa = fox2(foxes.weight, foxes.avgfood, foxes.area);
model_fg = fox2(foxes.weight, foxes.avgfood, foxes.groupsize);
model_fga = fox3(foxes.weight, foxes.avgfood, foxes.groupsize, foxes.area);
post_f = sample(model_f, NUTS(), 10_000);
post_g = sample(model_g, NUTS(), 10_000);
post_fa = sample(model_fa, NUTS(), 10_000);
post_fg = sample(model_fg, NUTS(), 10_000);
post_fga = sample(model_fga, NUTS(), 10_000);
psis_loo(model_f, post_f, source=:mcmc) # -166.60
psis_loo(model_g, post_g, source=:mcmc) # -165.24
psis_loo(model_fa, post_fa, source=:mcmc) # -167.17
psis_loo(model_fg, post_fg, source=:mcmc) # -161.78
psis_loo(model_fga, post_fga, source=:mcmc) # -161.43
3. Build a predictive model of the relationship show on the cover of the book, the relationship between the timing of cherry blossoms and March temperature in the same year. The data are in cherry_blossoms. Consider at least two functions to predict doy with temp. Compare them with PSIS or WAIC.
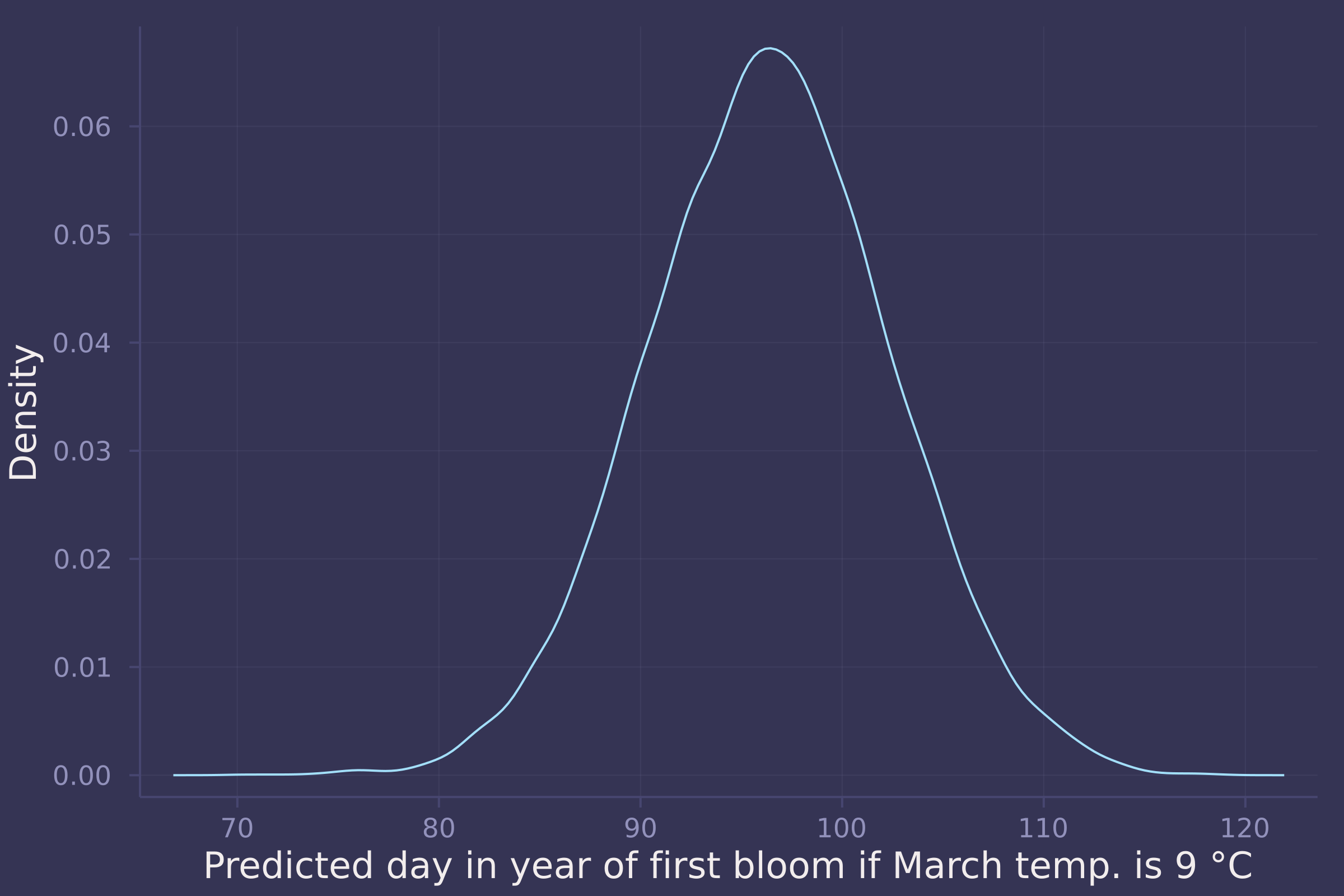
Suppose March temperatures reach 9 degrees by the year 2050. What does your best model predict for the predictive distribution of the day-in-year the cherry trees will blossom?
blossoms = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/cherry_blossoms.csv"),
DataFrame,
delim=';',
missingstring="NA"
)
## 1215×5 DataFrame
## Row │ year doy temp temp_upper temp_lower
## │ Int64 Int64? Float64? Float64? Float64?
## ──────┼──────────────────────────────────────────────────
## 1 │ 801 missing missing missing missing
## 2 │ 802 missing missing missing missing
## 3 │ 803 missing missing missing missing
## 4 │ 804 missing missing missing missing
## 5 │ 805 missing missing missing missing
## 6 │ 806 missing missing missing missing
## 7 │ 807 missing missing missing missing
## 8 │ 808 missing missing missing missing
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮
## 1209 │ 2009 95 missing missing missing
## 1210 │ 2010 95 missing missing missing
## 1211 │ 2011 99 missing missing missing
## 1212 │ 2012 101 missing missing missing
## 1213 │ 2013 93 missing missing missing
## 1214 │ 2014 94 missing missing missing
## 1215 │ 2015 93 missing missing missing
## 1200 rows omitted
dropmissing!(blossoms, [:doy, :temp])
## 787×5 DataFrame
## Row │ year doy temp temp_upper temp_lower
## │ Int64 Int64 Float64 Float64? Float64?
## ─────┼───────────────────────────────────────────────
## 1 │ 851 108 7.38 12.1 2.66
## 2 │ 864 100 6.42 8.69 4.14
## 3 │ 866 106 6.44 8.11 4.77
## 4 │ 889 104 6.83 8.48 5.19
## 5 │ 891 109 6.98 8.96 5.0
## 6 │ 892 108 7.11 9.11 5.11
## 7 │ 894 106 6.98 8.4 5.55
## 8 │ 895 104 7.08 8.57 5.58
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮
## 781 │ 1974 99 8.18 8.78 7.58
## 782 │ 1975 100 8.18 8.76 7.6
## 783 │ 1976 99 8.2 8.77 7.63
## 784 │ 1977 93 8.22 8.78 7.66
## 785 │ 1978 104 8.2 8.78 7.61
## 786 │ 1979 97 8.28 8.83 7.73
## 787 │ 1980 102 8.3 8.86 7.74
## 772 rows omitted
plot(blossoms.temp, blossoms.doy, ylab="Day in year of first blossom", xlab="March temperature (°C)", seriestype=:scatter, legend=false)
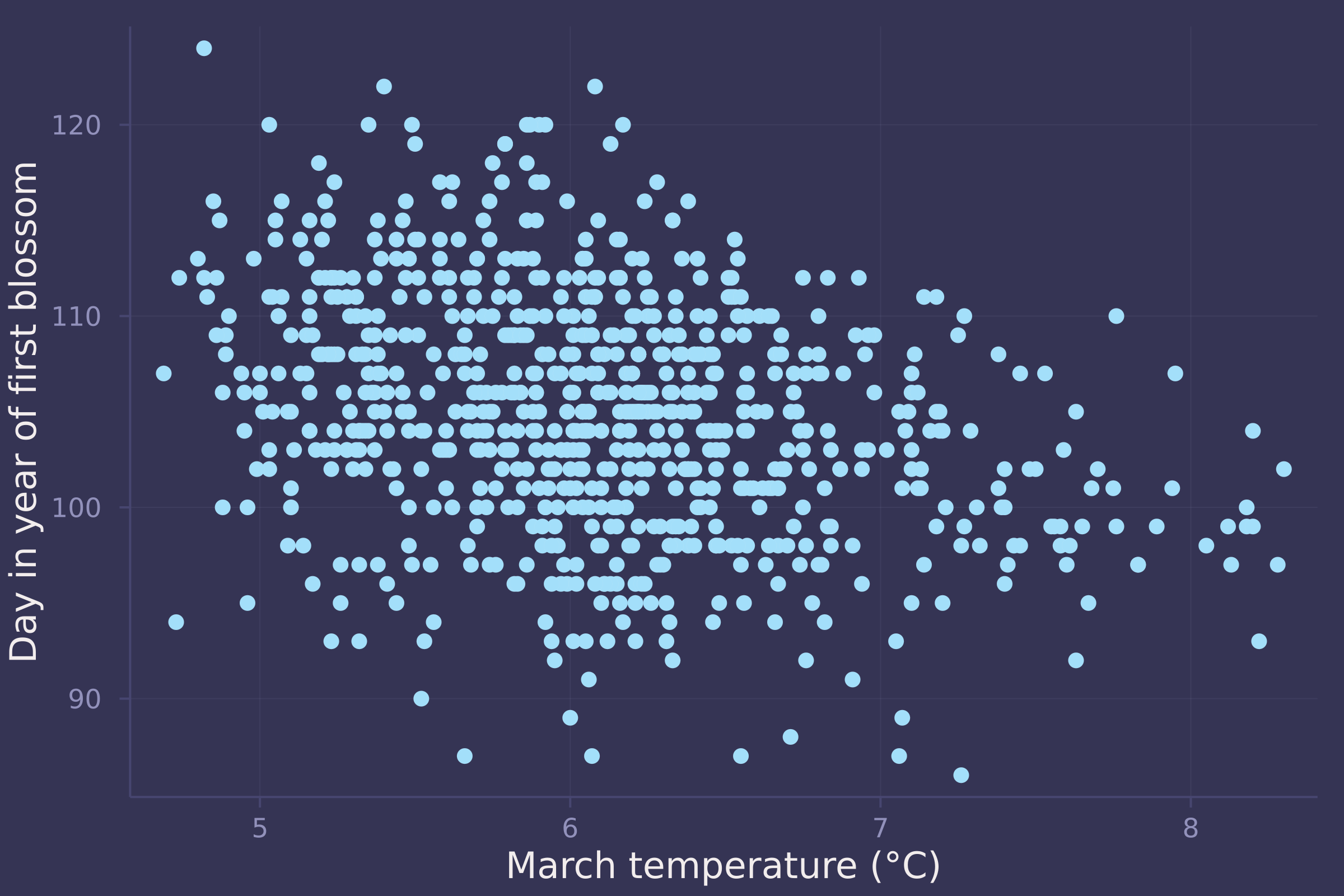
mean_doy = mean(blossoms.doy);
std_doy = std(blossoms.doy);
blossoms.doy = standardize(blossoms.doy);
mean_temp = mean(blossoms.temp);
std_temp = std(blossoms.temp);
blossoms.temp = standardize(blossoms.temp);
@model function blossom_line(d, t)
α ~ Normal(0, 0.2)
β ~ Normal(0, 0.5)
σ ~ Exponential(1)
μ = α .+ β .* t
d .~ Normal.(μ, σ)
end;
model_line = blossom_line(blossoms.doy, blossoms.temp);
post_line = sample(model_line, NUTS(), 10_000)
## Chains MCMC chain (10000×15×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 4.06 seconds
## Compute duration = 4.06 seconds
## parameters = α, β, σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α 0.0002 0.0328 0.0003 0.0002 17025.7063 1.0000 ⋯
## β -0.3252 0.0341 0.0003 0.0003 12714.6852 1.0001 ⋯
## σ 0.9464 0.0237 0.0002 0.0002 15815.9987 0.9999 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α -0.0650 -0.0213 0.0002 0.0220 0.0646
## β -0.3920 -0.3484 -0.3254 -0.3023 -0.2571
## σ 0.9012 0.9302 0.9460 0.9620 0.9946
@model function blossom_splines(d, B)
α ~ Normal(0, 0.2)
β ~ filldist(Normal(0, 0.5), size(B, 2))
σ ~ Exponential(1)
μ = α .+ B * β
@. d ~ Normal(μ, σ)
end;
n_knots = 10;
breakpoints = range(extrema(blossoms.temp)..., length=n_knots);
basis = BSplineBasis(4, breakpoints);
B = basismatrix(basis, blossoms.temp);
model_splines = blossom_splines(blossoms.doy, B);
post_splines = sample(model_splines, NUTS(), 10_000)
## Chains MCMC chain (10000×26×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 29.45 seconds
## Compute duration = 29.45 seconds
## parameters = α, β[1], β[2], β[3], β[4], β[5], β[6], β[7], β[8], β[9], β[10], β[11], β[12], σ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α -0.0920 0.1246 0.0012 0.0019 5108.6872 1.0000 ⋯
## β[1] 0.2760 0.3875 0.0039 0.0033 12795.9630 0.9999 ⋯
## β[2] 0.7123 0.3345 0.0033 0.0032 10393.2794 0.9999 ⋯
## β[3] 0.3454 0.2635 0.0026 0.0030 8340.9922 1.0001 ⋯
## β[4] 0.5412 0.2152 0.0022 0.0025 7627.4806 1.0000 ⋯
## β[5] 0.1595 0.1895 0.0019 0.0022 7354.2051 1.0002 ⋯
## β[6] -0.0165 0.1950 0.0020 0.0023 7583.9913 0.9999 ⋯
## β[7] -0.2038 0.2202 0.0022 0.0025 8218.6683 0.9999 ⋯
## β[8] -0.3293 0.2631 0.0026 0.0026 9071.6733 1.0000 ⋯
## β[9] -0.6002 0.3069 0.0031 0.0033 9888.1501 1.0001 ⋯
## β[10] -0.4692 0.3845 0.0038 0.0039 10985.7487 1.0000 ⋯
## β[11] -0.4978 0.4036 0.0040 0.0039 13242.1135 1.0000 ⋯
## β[12] -0.4522 0.3939 0.0039 0.0034 13846.2617 1.0001 ⋯
## σ 0.9505 0.0241 0.0002 0.0002 15595.1343 1.0001 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α -0.3364 -0.1757 -0.0924 -0.0095 0.1543
## β[1] -0.4796 0.0200 0.2770 0.5403 1.0330
## β[2] 0.0638 0.4851 0.7111 0.9404 1.3618
## β[3] -0.1765 0.1700 0.3477 0.5150 0.8650
## β[4] 0.1226 0.3963 0.5395 0.6861 0.9674
## β[5] -0.2101 0.0320 0.1594 0.2902 0.5289
## β[6] -0.3900 -0.1477 -0.0192 0.1163 0.3688
## β[7] -0.6345 -0.3535 -0.2031 -0.0538 0.2251
## β[8] -0.8527 -0.5060 -0.3288 -0.1523 0.1810
## β[9] -1.1981 -0.8084 -0.5997 -0.3943 0.0043
## β[10] -1.2143 -0.7340 -0.4683 -0.2046 0.2831
## β[11] -1.2896 -0.7674 -0.5000 -0.2315 0.3007
## β[12] -1.2090 -0.7199 -0.4528 -0.1860 0.3177
## σ 0.9045 0.9341 0.9502 0.9664 0.9987
psis_loo(model_line, post_line, source=:mcmc); # -1074.60
psis_loo(model_splines, post_splines, source=:mcmc); # -1080.86
temp_seq = collect(range(-3, 5, length=100));
μ_post = post_line["α"] .+ post_line["β"] * temp_seq';
plot(std_temp .* blossoms.temp .+ mean_temp, std_doy .* blossoms.doy .+ mean_doy, ylab="Day in year of first blossom", xlab="March temperature (°C)", seriestype=:scatter, legend=false, alpha=0.4);
plot!(std_temp .* temp_seq .+ mean_temp, std_doy .* vec(mean(μ_post, dims=1)) .+ mean_doy, legend=false)
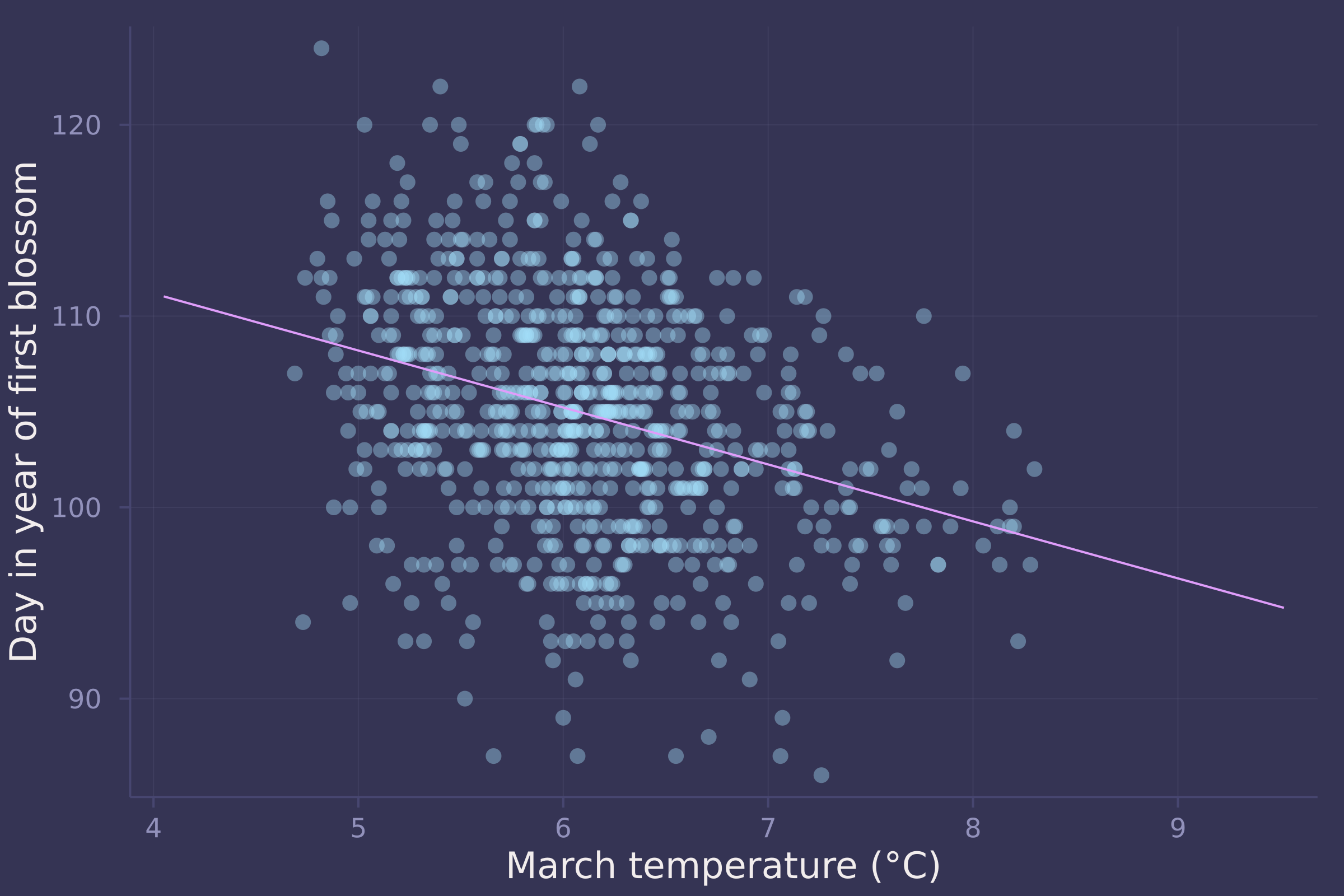
μ_post_at_temp_9C = rand.(Normal.(post_line["α"] .+ post_line["β"] .* (9 .- mean_temp) ./ std_temp, post_line["σ"]));
density(std_doy .* μ_post_at_temp_9C .+ mean_doy, ylab="Density", xlab="Predicted day in year of first bloom if March temp. is 9 °C", legend=false)
Homework 5
1. The data in grants are outcomes for scientific funding applications for the Netherlands Organization for Scientific Research (NWO) from 2010–2012. (see van der Lee and Ellemers <doi:10.1073/pnas.1510159112>). These data have a similar structure to the UCB admissions data discussed in Chapter 11. Draw a DAG for this sample and then use one or more binomial GLMs to estimate the total causal effect of gender on grant awards.
Let G represent the gender of the grant applicant, D represent the discipline of the grant application, and A represent whether or not the grant was awarded.
invlogit(x) = exp(x) / (1 + exp(x));
grants = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/NWOGrants.csv"),
DataFrame,
delim=';'
)
## 18×4 DataFrame
## Row │ discipline gender applications awards
## │ String31 String1 Int64 Int64
## ─────┼────────────────────────────────────────────────────
## 1 │ Chemical sciences m 83 22
## 2 │ Chemical sciences f 39 10
## 3 │ Physical sciences m 135 26
## 4 │ Physical sciences f 39 9
## 5 │ Physics m 67 18
## 6 │ Physics f 9 2
## 7 │ Humanities m 230 33
## 8 │ Humanities f 166 32
## ⋮ │ ⋮ ⋮ ⋮ ⋮
## 12 │ Interdisciplinary f 78 17
## 13 │ Earth/life sciences m 156 38
## 14 │ Earth/life sciences f 126 18
## 15 │ Social sciences m 425 65
## 16 │ Social sciences f 409 47
## 17 │ Medical sciences m 245 46
## 18 │ Medical sciences f 260 29
## 3 rows omitted
grants.gender = [gender == "f" ? 1 : 2 for gender in grants.gender];
disciplines = unique(grants.discipline);
grants.discipline = [
findfirst(d -> d == discipline, disciplines)
for discipline in grants.discipline
];
@model function grant_gender_on_award_total(a, g, n)
α ~ filldist(Normal(0, 1.5), 2)
p = invlogit.(α[g])
a .~ Binomial.(n, p)
end;
model_total = grant_gender_on_award_total(
grants.awards,
grants.gender,
grants.applications
);
post_total = sample(model_total, NUTS(), 10_000)
## Chains MCMC chain (10000×14×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 7.75 seconds
## Compute duration = 7.75 seconds
## parameters = α[1], α[2]
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α[1] -1.7383 0.0823 0.0008 0.0009 9852.4335 0.9999 ⋯
## α[2] -1.5330 0.0644 0.0006 0.0005 10554.9990 1.0000 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α[1] -1.9014 -1.7942 -1.7368 -1.6832 -1.5792
## α[2] -1.6601 -1.5769 -1.5320 -1.4894 -1.4077
gender_adv_total = invlogit.(post_total["α[2]"]) - invlogit.(post_total["α[1]"]);
density(gender_adv_total, ylab="Density", xlab="Gender contrast (probability)", legend=false);
plot!([0, 0], [0, 34], line=:dash, color=:white);
annotate!(-0.005, 32, text("women advantaged", :white, :right, 8));
annotate!(0.005, 32, text("men advantaged", :white, :left, 8))
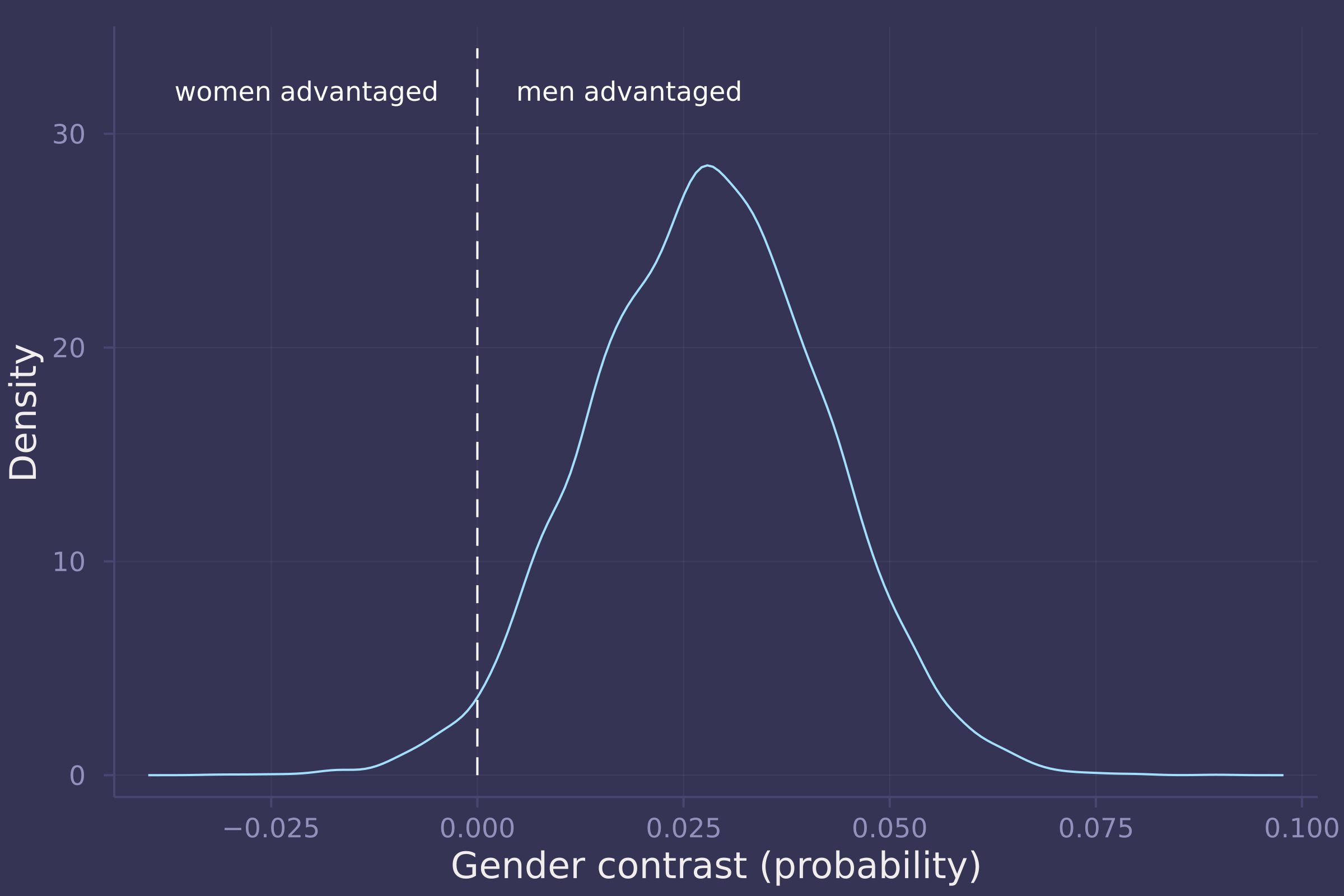
2. Now estimate the direct causal effect of gender on grant awards. Compute the average direct causal effect of gender, weighting each discipline in proportion to the number of applications in the sample. Refer to the marginal effect example in Lecture 9 for help.
@model function grant_gender_on_award_direct(a, g, n, d)
α ~ filldist(Normal(0, 1.5), length(unique(g)), length(unique(d)))
for i in 1:length(a)
a[i] ~ Binomial(n[i], invlogit(α[g[i], d[i]]))
end
end;
model_direct = grant_gender_on_award_direct(
grants.awards,
grants.gender,
grants.applications,
grants.discipline
);
post_direct = sample(model_direct, NUTS(), 10_000)
## Chains MCMC chain (10000×30×1 Array{Float64, 3}):
##
## Iterations = 1001:1:11000
## Number of chains = 1
## Samples per chain = 10000
## Wall duration = 4.78 seconds
## Compute duration = 4.78 seconds
## parameters = α[1,1], α[2,1], α[1,2], α[2,2], α[1,3], α[2,3], α[1,4], α[2,4], α[1,5], α[2,5], α[1,6], α[2,6], α[1,7], α[2,7], α[1,8], α[2,8], α[1,9], α[2,9]
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α[1,1] -1.0354 0.3565 0.0036 0.0027 17314.5238 0.9999 ⋯
## α[2,1] -1.0055 0.2426 0.0024 0.0017 16975.3056 1.0001 ⋯
## α[1,2] -1.1640 0.3646 0.0036 0.0030 14896.8231 1.0000 ⋯
## α[2,2] -1.4197 0.2212 0.0022 0.0018 15476.4679 0.9999 ⋯
## α[1,3] -1.0686 0.6990 0.0070 0.0053 16916.5101 0.9999 ⋯
## α[2,3] -0.9901 0.2763 0.0028 0.0023 16650.9139 0.9999 ⋯
## α[1,4] -1.4195 0.1938 0.0019 0.0016 18235.8213 0.9999 ⋯
## α[2,4] -1.7713 0.1867 0.0019 0.0014 15472.5930 0.9999 ⋯
## α[1,5] -1.2981 0.3077 0.0031 0.0022 16814.2082 0.9999 ⋯
## α[2,5] -1.6534 0.1953 0.0020 0.0015 16313.0272 0.9999 ⋯
## α[1,6] -1.2575 0.2727 0.0027 0.0021 17493.6539 1.0001 ⋯
## α[2,6] -1.9976 0.2970 0.0030 0.0024 17122.6507 1.0001 ⋯
## α[1,7] -1.7645 0.2512 0.0025 0.0016 19403.7417 0.9999 ⋯
## α[2,7] -1.1263 0.1853 0.0019 0.0014 20398.8360 0.9999 ⋯
## α[1,8] -2.0284 0.1535 0.0015 0.0014 14443.1747 0.9999 ⋯
## α[2,8] -1.7047 0.1320 0.0013 0.0009 17872.9843 0.9999 ⋯
## α[1,9] -2.0521 0.1935 0.0019 0.0014 20877.7466 0.9999 ⋯
## α[2,9] -1.4575 0.1642 0.0016 0.0012 19516.6949 0.9999 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α[1,1] -1.7650 -1.2663 -1.0244 -0.7895 -0.3700
## α[2,1] -1.4856 -1.1677 -1.0000 -0.8394 -0.5447
## α[1,2] -1.9138 -1.3993 -1.1510 -0.9162 -0.4844
## α[2,2] -1.8670 -1.5689 -1.4159 -1.2702 -0.9980
## α[1,3] -2.5336 -1.5215 -1.0411 -0.5953 0.2414
## α[2,3] -1.5518 -1.1774 -0.9813 -0.8001 -0.4703
## α[1,4] -1.8128 -1.5487 -1.4144 -1.2878 -1.0526
## α[2,4] -2.1513 -1.8963 -1.7662 -1.6446 -1.4145
## α[1,5] -1.9183 -1.4995 -1.2913 -1.0873 -0.7207
## α[2,5] -2.0521 -1.7784 -1.6465 -1.5223 -1.2849
## α[1,6] -1.8120 -1.4371 -1.2509 -1.0728 -0.7437
## α[2,6] -2.6055 -2.1927 -1.9856 -1.7926 -1.4437
## α[1,7] -2.2604 -1.9313 -1.7592 -1.5887 -1.2964
## α[2,7] -1.4985 -1.2483 -1.1249 -1.0006 -0.7719
## α[1,8] -2.3439 -2.1274 -2.0226 -1.9249 -1.7398
## α[2,8] -1.9689 -1.7928 -1.7031 -1.6146 -1.4503
## α[1,9] -2.4342 -2.1809 -2.0468 -1.9189 -1.6866
## α[2,9] -1.7929 -1.5640 -1.4528 -1.3469 -1.1426
gender_adv_direct = [
invlogit.(post_direct["α[2,$i]"]) -
invlogit.(post_direct["α[1,$i]"])
for i in 1:length(disciplines)
];
gender_adv_direct = hcat(gender_adv_direct...);
density(gender_adv_direct[:, 1:5], ylab="Density", xlab="Gender contrast (probability)", labels=["Chemical sciences" "Physical sciences" "Physics" "Humanities" "Technical sciences"], legend=:left);
plot!([0, 0], [0, 15], line=:dash, color=:white, label="");
annotate!(-0.025, 13, text("women advantaged", :white, :right, 8));
annotate!(0.025, 13, text("men advantaged", :white, :left, 8))
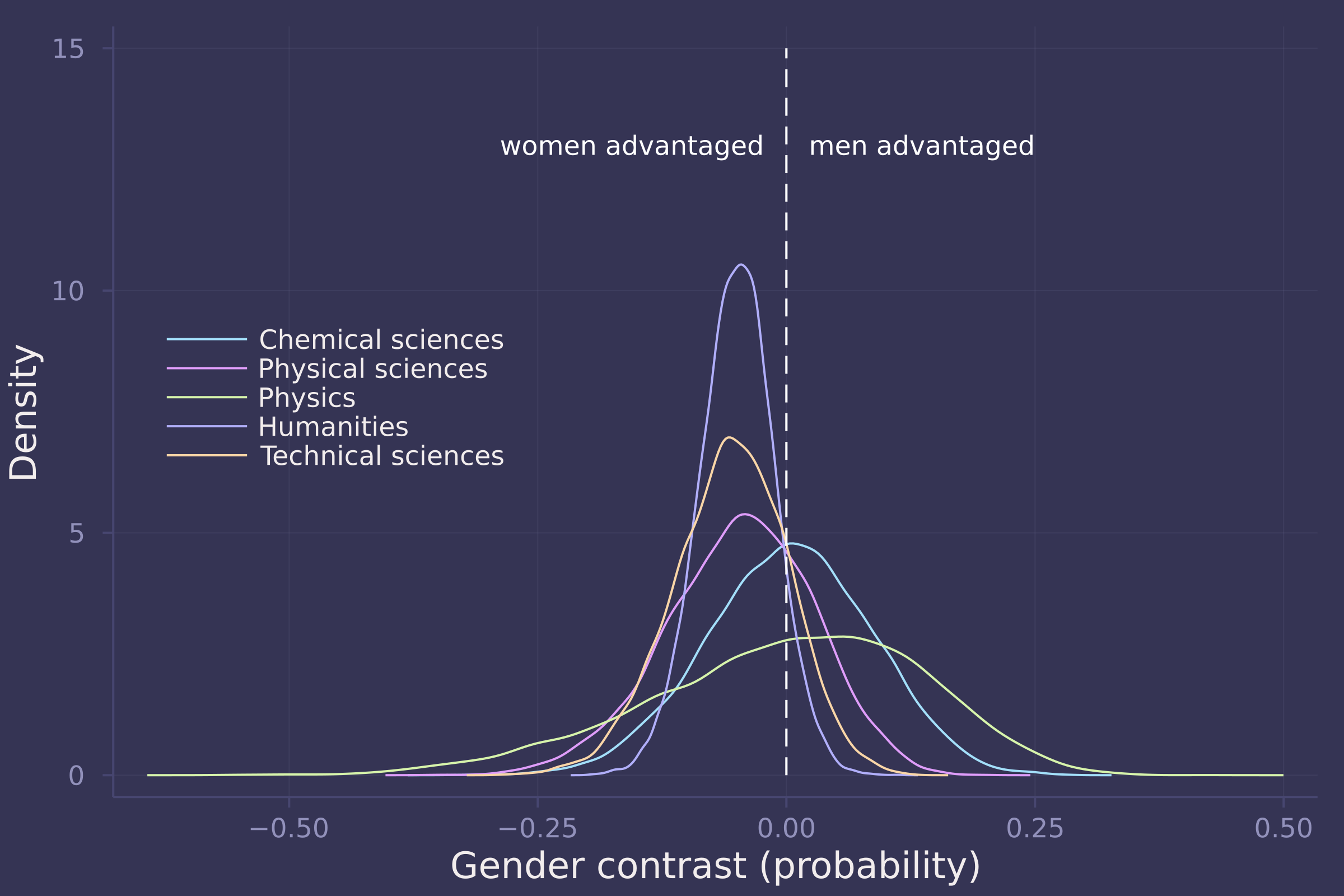
density(gender_adv_direct[:, 6:9], ylab="Density", xlab="Gender contrast (probability)", labels=["Interdisciplinary" "Earth/life sciences" "Social sciences" "Medical sciences"], legend=:left);
plot!([0, 0], [0, 21], line=:dash, color=:white, label="");
annotate!(-0.025, 19, text("women advantaged", :white, :right, 8));
annotate!(0.025, 19, text("men advantaged", :white, :left, 8))
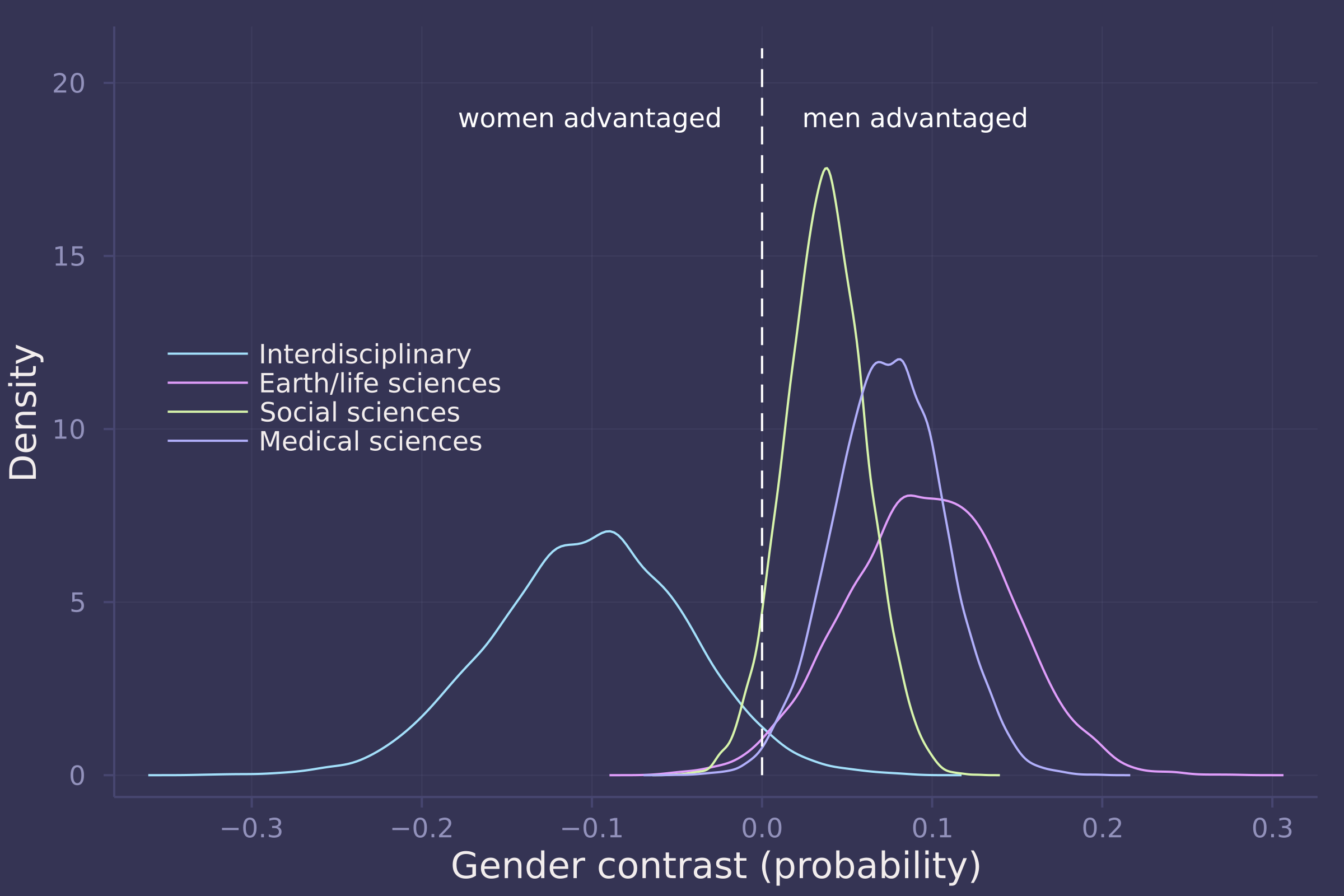
3. Considering the total effect (problem 1) and direct effect (problem 2) of gender, what causes contribute to the average difference between women and men in award rate in this sample? It is not necessary to say whether or not there is evidence of discrimination. Simply explain how the direct effects you have estimated make sense (or not) of the total effect.
Homework 6
The theme of this homework is tadpoles. You must keep them alive.
1. Conduct a prior predictive simulation for the Reedfrog model. By this I mean to simulate the prior distribution of tank survival probabilities αj . Start by using this prior:
Be sure to transform the αj values to the probability scale for plotting and summary. How does increasing the width of the prior on σ change the prior distribution αj ? You might try Exponential(10) and Exponential(0.1) for example.
# redefine a version of invlogit that's more computationally stable
invlogit(x) = exp(x - log(1 + exp(x)));
σ_dists = [Exponential(0.1), Exponential(1), Exponential(10)];
function sim_priors(σ_dist, n=10_000)
σ = rand(σ_dist, n)
ᾱ = rand(Normal(0, 1), n)
α = rand.(Normal.(ᾱ, σ))
invlogit.(α)
end;
sims = hcat(sim_priors.(σ_dists)...);
density(sims, xlims=[0.025, 0.975], ylab="Density",xlab="Simulated prior survival probability", labels=["Exp(0.1)" "Exp(1)" "Exp(10)"], legend=:top)
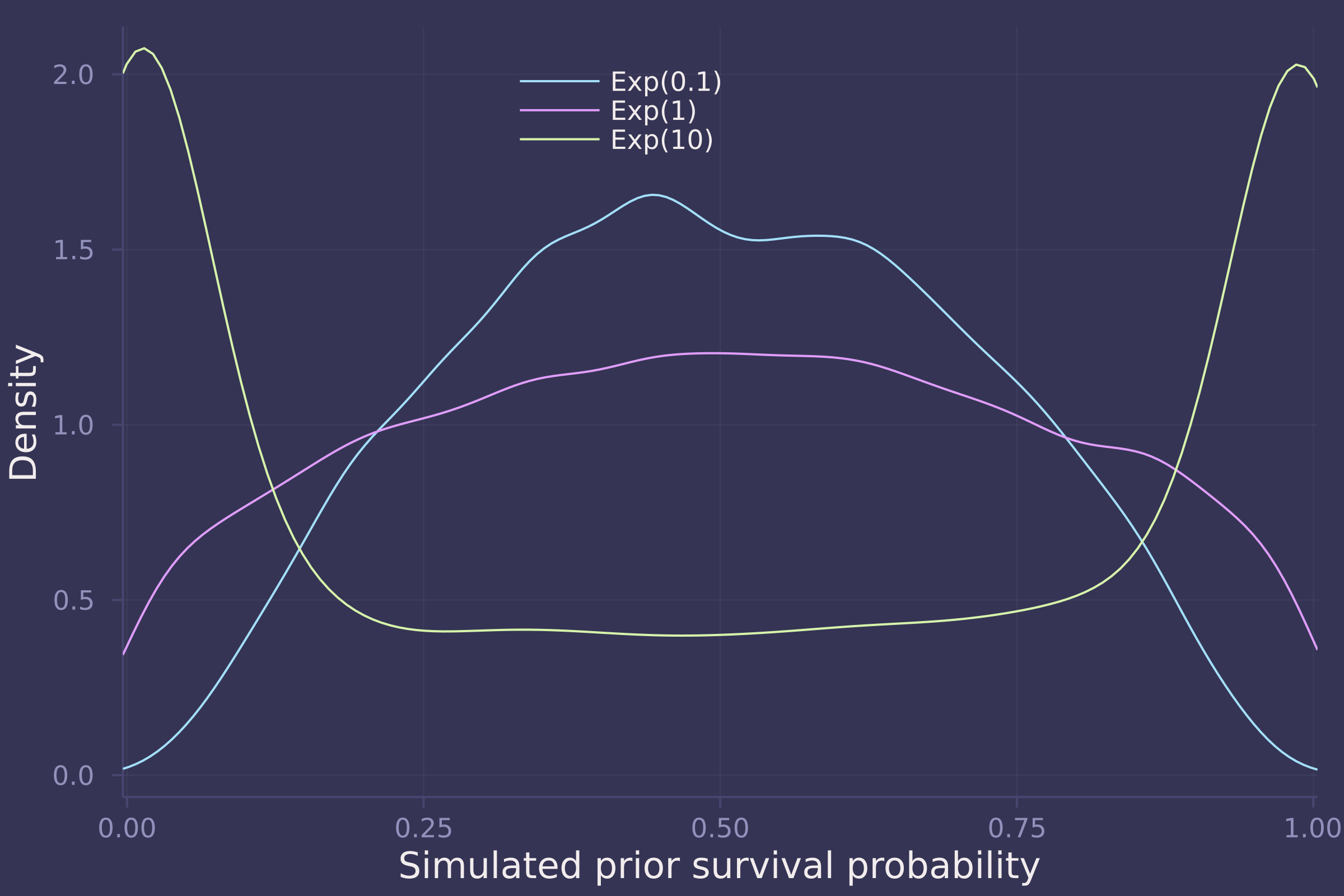
2. Revisit the Reedfrog survival data. Start with the varying effects model from the book and the lecture. Then modify it to estimate the causal effects of the treatement variables pred and size, including how size might modify the effect of predation. An easy approach is to estimate the effect for each combination of pred and size. Justify your model with a DAG of this experiment.
tadpoles = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/reedfrogs.csv"),
DataFrame,
delim=';'
)
## 48×5 DataFrame
## Row │ density pred size surv propsurv
## │ Int64 String7 String7 Int64 Float64
## ─────┼────────────────────────────────────────────
## 1 │ 10 no big 9 0.9
## 2 │ 10 no big 10 1.0
## 3 │ 10 no big 7 0.7
## 4 │ 10 no big 10 1.0
## 5 │ 10 no small 9 0.9
## 6 │ 10 no small 9 0.9
## 7 │ 10 no small 10 1.0
## 8 │ 10 no small 9 0.9
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮
## 42 │ 35 pred big 12 0.342857
## 43 │ 35 pred big 13 0.371429
## 44 │ 35 pred big 14 0.4
## 45 │ 35 pred small 22 0.628571
## 46 │ 35 pred small 12 0.342857
## 47 │ 35 pred small 31 0.885714
## 48 │ 35 pred small 17 0.485714
## 33 rows omitted
tadpoles.tank = collect(1:size(tadpoles, 1));
tadpoles.pred = [pred == "no" ? 1 : 2 for pred in tadpoles.pred];
tadpoles.size = [size == "small" ? 1 : 2 for size in tadpoles.size];
@model function survival_vareff(surv, density, tank, pred, size)
σ ~ Exponential(1)
ᾱ ~ Normal(0, 1.5)
α ~ filldist(Normal(ᾱ, σ), length(unique(tank)))
β ~ filldist(Normal(0, 1.5), length(unique(pred)), length(unique(size)))
for i in 1:length(surv)
surv[i] ~ Binomial(density[i], invlogit(α[i] + β[pred[i], size[i]]))
end
end;
model_vareff = survival_vareff(
tadpoles.surv,
tadpoles.density,
tadpoles.tank,
tadpoles.pred,
tadpoles.size
);
post_vareff = sample(model_vareff, NUTS(), 10_000);
βs = ["β[1,1]", "β[1,2]", "β[2,1]", "β[2,2]"];
density([post_vareff[β] for β in βs], ylab="Density", xlab="β", labels=["Small, no predators" "Big, no predators" "Small, predators" "Big, predators"], legend=:topleft);
plot!([0, 0], [0, 0.55], line=:dash, color=:white, label="")
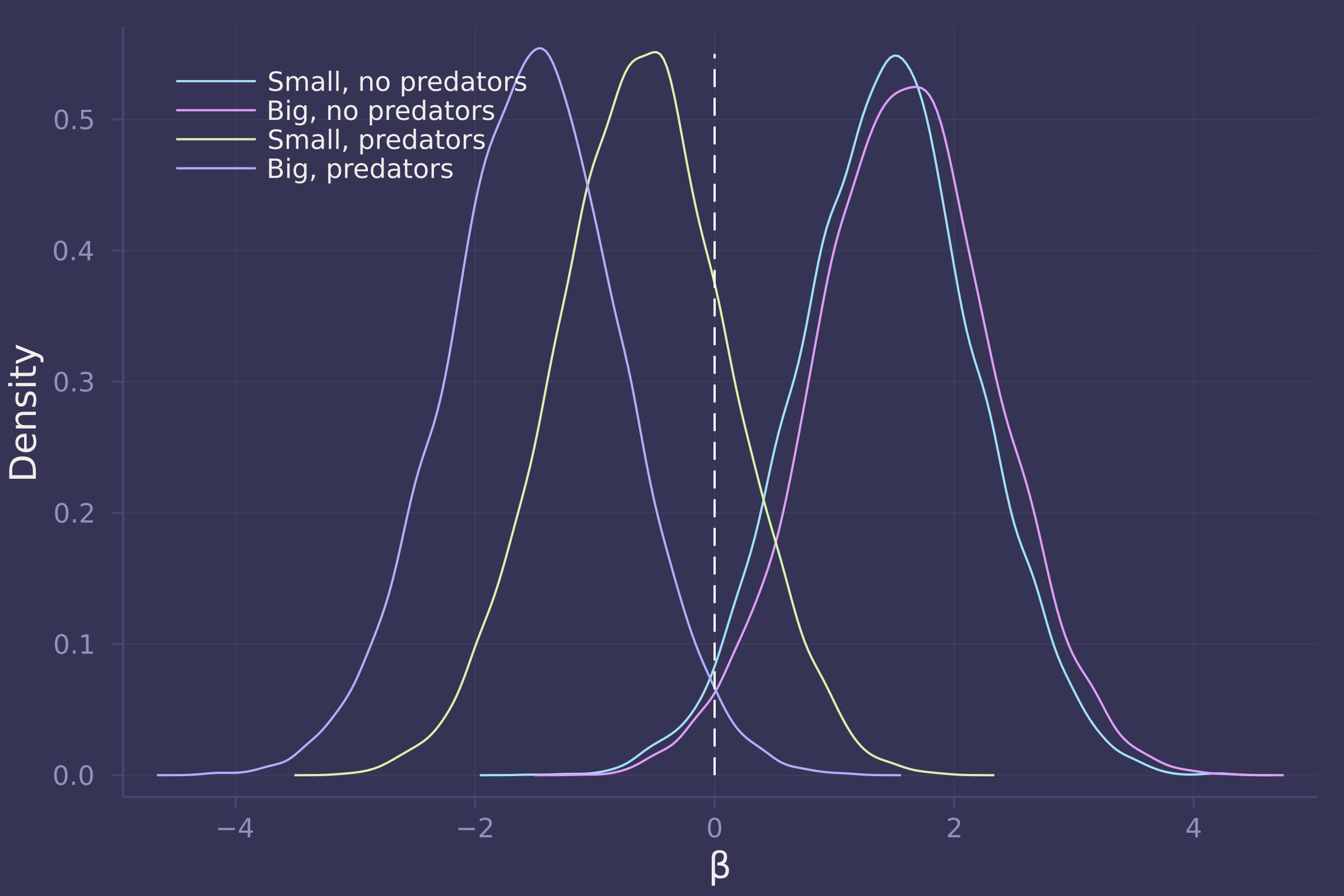
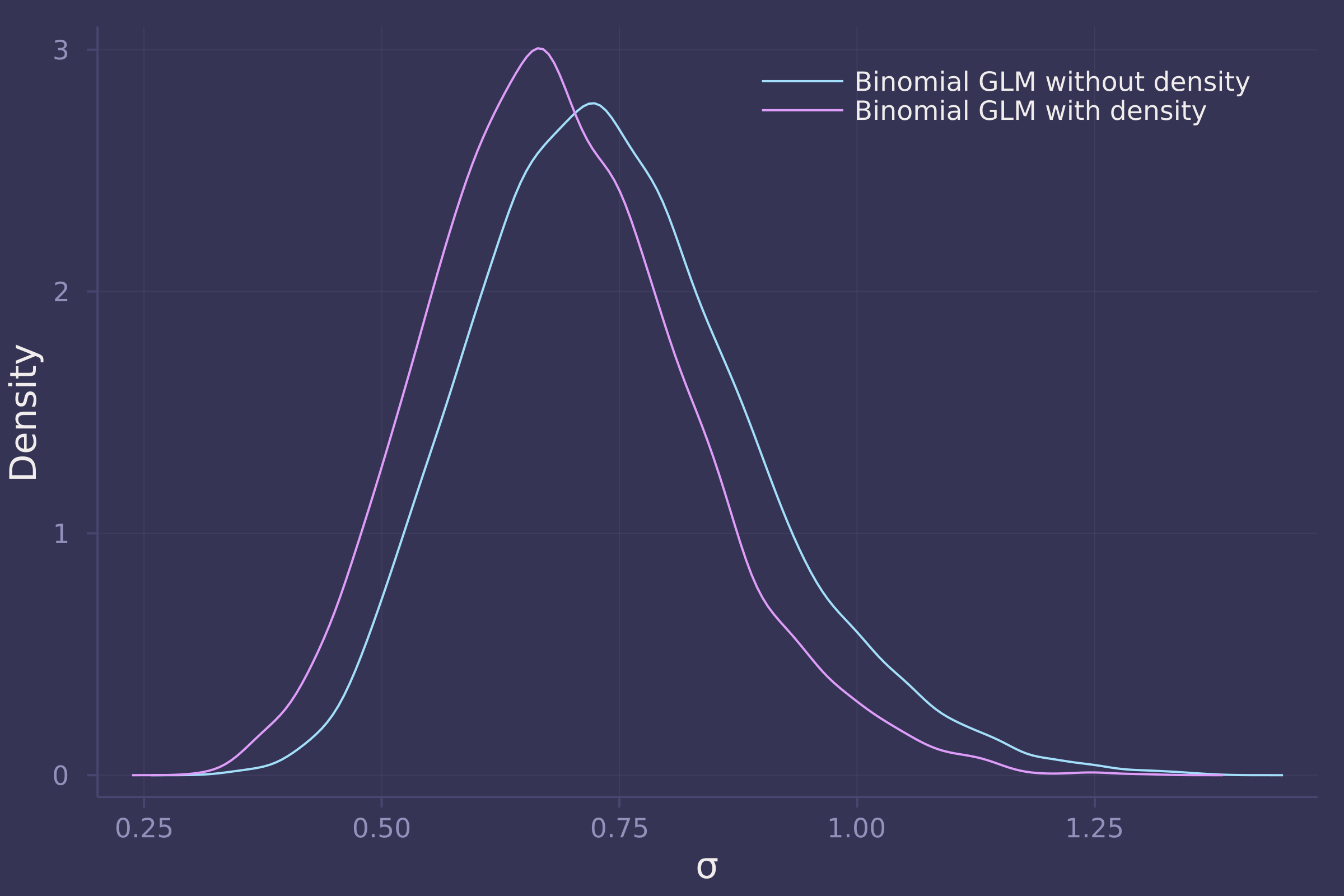
3. Now estimate the causal effect of density on survival. Consider whether pred modifies the effect of density. There are several good ways to include density in your Binomial GLM. You could treat it as a continuous regression variable (possibly standardized). Or you could convert it to an ordered category (with three levels). Compare the σ (tank standard deviation) posterior distribution to σ from your model in Problem 2. How are they different? Why?
@model function survival_with_density(surv, density, tank, pred, size)
σ ~ Exponential(1)
ᾱ ~ Normal(0, 1.5)
α ~ filldist(Normal(ᾱ, σ), length(unique(tank)))
β ~ filldist(Normal(0, 1.5), length(unique(pred)), length(unique(size)))
γ ~ filldist(Normal(0, 1.5), length(unique(pred)))
for i in 1:length(surv)
surv[i] ~ Binomial(density[i], invlogit(α[i] + β[pred[i], size[i]] + γ[pred[i]] * density[i]))
end
end;
model_with_density = survival_with_density(
tadpoles.surv,
tadpoles.density,
tadpoles.tank,
tadpoles.pred,
tadpoles.size
);
post_with_density = sample(model_with_density, NUTS(), 10_000);
βs = ["β[1,1]", "β[1,2]", "β[2,1]", "β[2,2]"];
density([post_with_density[β] for β in βs], ylab="Density", xlab="β", labels=["Small, no predators" "Big, no predators" "Small, predators" "Big, predators"], legend=:topleft);
plot!([0, 0], [0, 0.6], line=:dash, color=:white, label="")
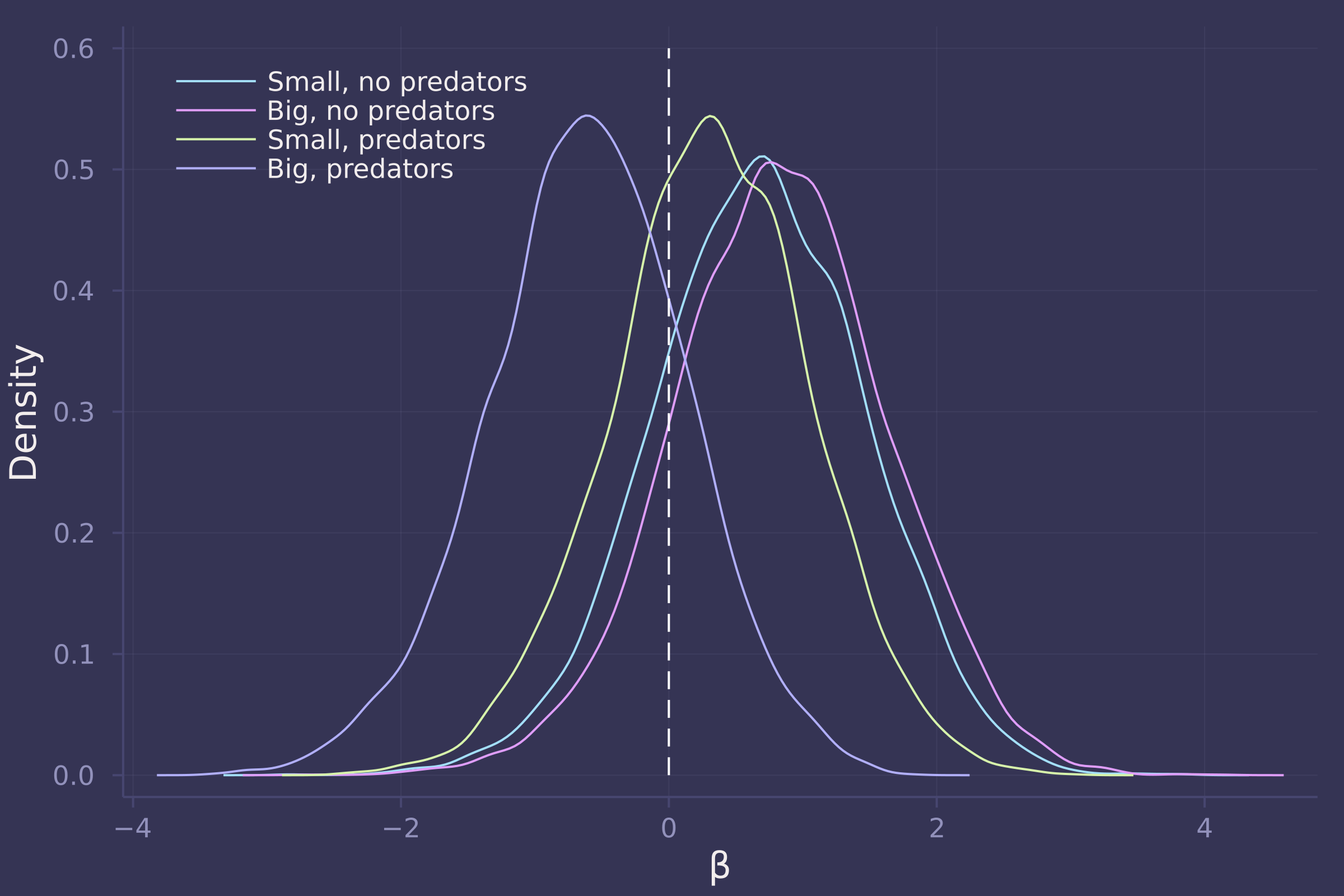
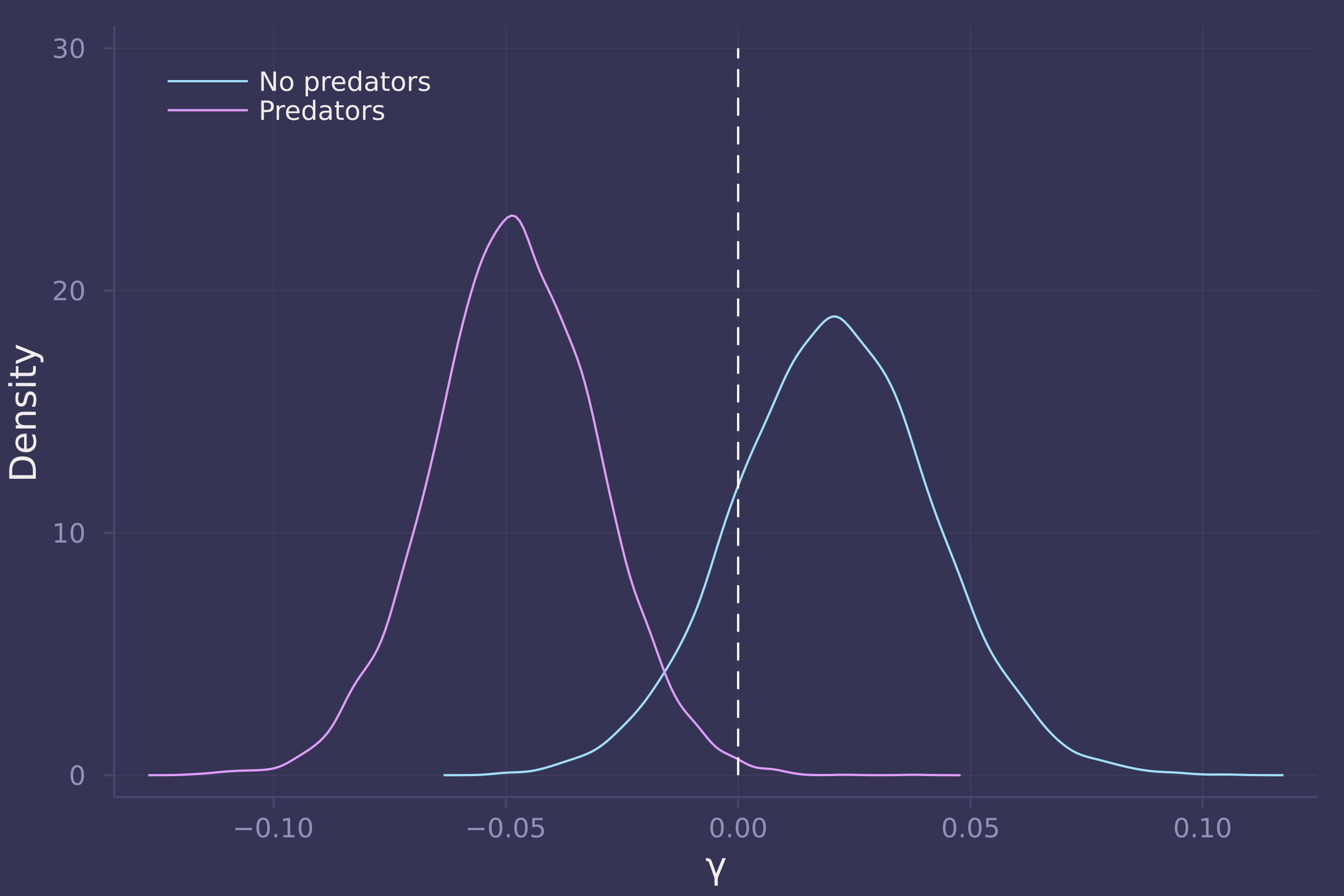
γs = ["γ[1]", "γ[2]"];
density([post_with_density[γ] for γ in γs], ylab="Density", xlab="γ", labels=["No predators" "Predators"], legend=:topleft);
plot!([0, 0], [0, 30], line=:dash, color=:white, label="")
density([post_vareff["σ"], post_with_density["σ"]], ylab="Density", xlab="σ", labels=["Binomial GLM without density" "Binomial GLM with density"])
Homework 7
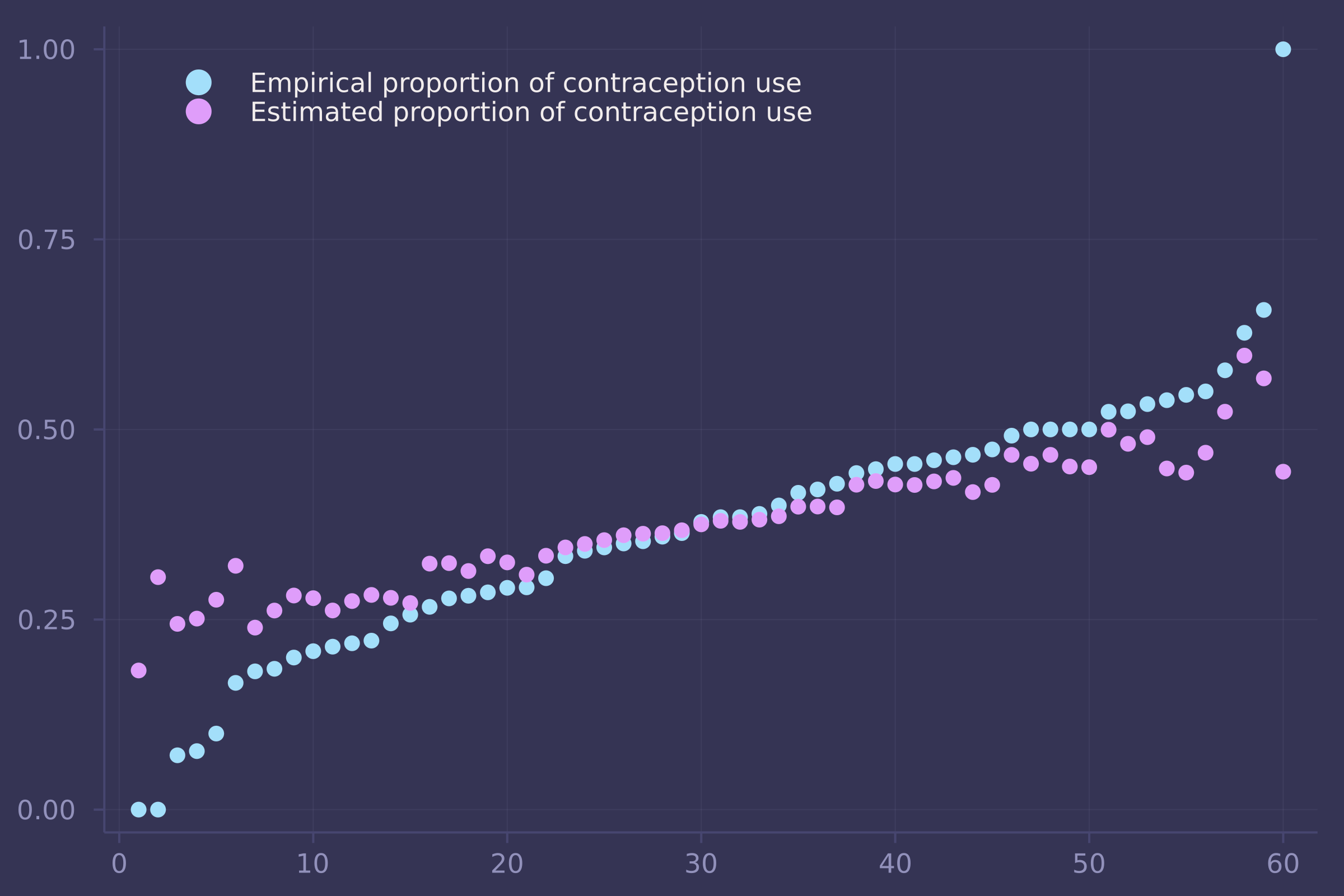
1. The data in bangladesh are 1934 women from the 1989 Bangladesh Fertility Survey. For each woman, we know which district she lived, her number of living_children, her age_centered, whether she lived in an urban center, and finally whether or not she used contraception (use_contraception). In the first problem, I only want you to investigate the proportion of women using contraception in each distirct. Use partial pooling (varying effects). Then compare the varying effects estimates to the raw empirical proportion in each district. Explain the differences between the estimates and the data. Note that district number 54 is absent in the data. This may cause some problems in indexing the parameters. Pay special attention to district number 54’s estimate.
bangladesh = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/bangladesh.csv"),
DataFrame,
delim=';'
);
rename!(
bangladesh,
"use.contraception" => :use_contraception,
"living.children" => :living_children,
"age.centered" => :age_centered
)
## 1934×6 DataFrame
## Row │ woman district use_contraception living_children age_centered urb ⋯
## │ Int64 Int64 Int64 Int64 Float64 Int ⋯
## ──────┼─────────────────────────────────────────────────────────────────────────
## 1 │ 1 1 0 4 18.44 ⋯
## 2 │ 2 1 0 1 -5.5599
## 3 │ 3 1 0 3 1.44
## 4 │ 4 1 0 4 8.44
## 5 │ 5 1 0 1 -13.559 ⋯
## 6 │ 6 1 0 1 -11.56
## 7 │ 7 1 0 4 18.44
## 8 │ 8 1 0 4 -3.5599
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱
## 1928 │ 1928 61 1 3 -9.5599 ⋯
## 1929 │ 1929 61 0 3 -2.5599
## 1930 │ 1930 61 0 4 14.44
## 1931 │ 1931 61 0 3 -4.5599
## 1932 │ 1932 61 0 4 14.44 ⋯
## 1933 │ 1933 61 0 1 -13.56
## 1934 │ 1934 61 0 4 10.44
## 1 column and 1919 rows omitted
bangladesh_districts = combine(
groupby(bangladesh, :district),
:woman => length => :n_total,
:use_contraception => sum => :n_use_contraception
)
## 60×3 DataFrame
## Row │ district n_total n_use_contraception
## │ Int64 Int64 Int64
## ─────┼────────────────────────────────────────
## 1 │ 1 117 30
## 2 │ 2 20 7
## 3 │ 3 2 2
## 4 │ 4 30 15
## 5 │ 5 39 14
## 6 │ 6 65 19
## 7 │ 7 18 5
## 8 │ 8 37 14
## ⋮ │ ⋮ ⋮ ⋮
## 54 │ 55 6 1
## 55 │ 56 45 26
## 56 │ 57 27 5
## 57 │ 58 33 15
## 58 │ 59 10 1
## 59 │ 60 32 7
## 60 │ 61 42 9
## 45 rows omitted
@model function bangladesh_district_contraception_use(d, n, k)
σ ~ Exponential(1)
ᾱ ~ Normal(0, 1.5)
α ~ filldist(Normal(ᾱ, σ), length(d))
k .~ Binomial.(n, invlogit.(α))
end;
model_bangladesh_district_contraception_use = bangladesh_district_contraception_use(
bangladesh_districts.district,
bangladesh_districts.n_total,
bangladesh_districts.n_use_contraception
);
post_bangladesh_district_contraception_use = sample(
model_bangladesh_district_contraception_use,
NUTS(),
10_000
);
post_p = invlogit.(
post_bangladesh_district_contraception_use[["α[$i]" for i in 1:length(bangladesh_districts.district)]].value
);
p_df = DataFrame(
district = bangladesh_districts.district,
estimate = vec(mean(post_p, dims=1)),
empirical = bangladesh_districts.n_use_contraception ./ bangladesh_districts.n_total
);
sort!(p_df, :empirical)
## 60×3 DataFrame
## Row │ district estimate empirical
## │ Int64 Float64 Float64
## ─────┼───────────────────────────────
## 1 │ 11 0.182979 0.0
## 2 │ 49 0.30574 0.0
## 3 │ 24 0.244268 0.0714286
## 4 │ 10 0.251211 0.0769231
## 5 │ 59 0.276014 0.1
## 6 │ 55 0.320645 0.166667
## 7 │ 27 0.23933 0.181818
## 8 │ 57 0.261808 0.185185
## ⋮ │ ⋮ ⋮ ⋮
## 54 │ 37 0.448628 0.538462
## 55 │ 42 0.443219 0.545455
## 56 │ 16 0.46939 0.55
## 57 │ 56 0.52331 0.577778
## 58 │ 14 0.597111 0.627119
## 59 │ 34 0.567127 0.657143
## 60 │ 3 0.444418 1.0
## 45 rows omitted
plot(1:nrow(p_df), [p_df.empirical p_df.estimate], seriestype=:scatter, labels=["Empirical proportion of contraception use" "Estimated proportion of contraception use"], legend=:topleft)
2. First, draw a DAG that includes all five variables. Use contraception C , Age A , Children K , Urban U , and District D . You don’t have to be an expert on fertility. But do think about which variables can influence which other variables. Second, design an estimation strategy to identify both the total and direct causal effects of living in an urban center on contraceptive use. Those are your estimands. Consider causal relationships among the variables. Then use your DAG to justify an adjustment set that will yield the estimate of the causal effect of urban living on contraceptive use. Do not run a statistical model (yet). I just want you to try to design an analysis. There is no firm right answer. Just apply the backdoor criterion and rules of d-separation (the elemental confounds) correctly to the DAG you design.
3. Now build one or more statistical models to estimate the total and the direct causal effects of urban living on contraceptive use. Again include district as a simple varying effect (as in problem 1) so that each district has its own average contraceptive use. You may also want to stratify the effect of urban living by district. If you do, think carefully about how to do this statistically.
@model function bangladesh_urban_on_contraception_use_total(c, u, d, n_districts)
σ ~ Exponential(1)
ᾱ ~ Normal(0, 1.5)
α ~ filldist(Normal(ᾱ, σ), n_districts)
β ~ Normal(0, 0.5)
for i in 1:length(c)
c[i] ~ Bernoulli(invlogit(α[d[i]] + β * u[i]))
end
end;
model_bangladesh_urban_on_contraception_use_total = bangladesh_urban_on_contraception_use_total(
bangladesh.use_contraception,
bangladesh.urban,
bangladesh.district,
maximum(bangladesh.district)
);
post_bangladesh_urban_on_contraception_use_total = sample(
model_bangladesh_urban_on_contraception_use_total,
NUTS(),
5_000
);
density(post_bangladesh_urban_on_contraception_use_total[:β], xlab="β", legend=false)
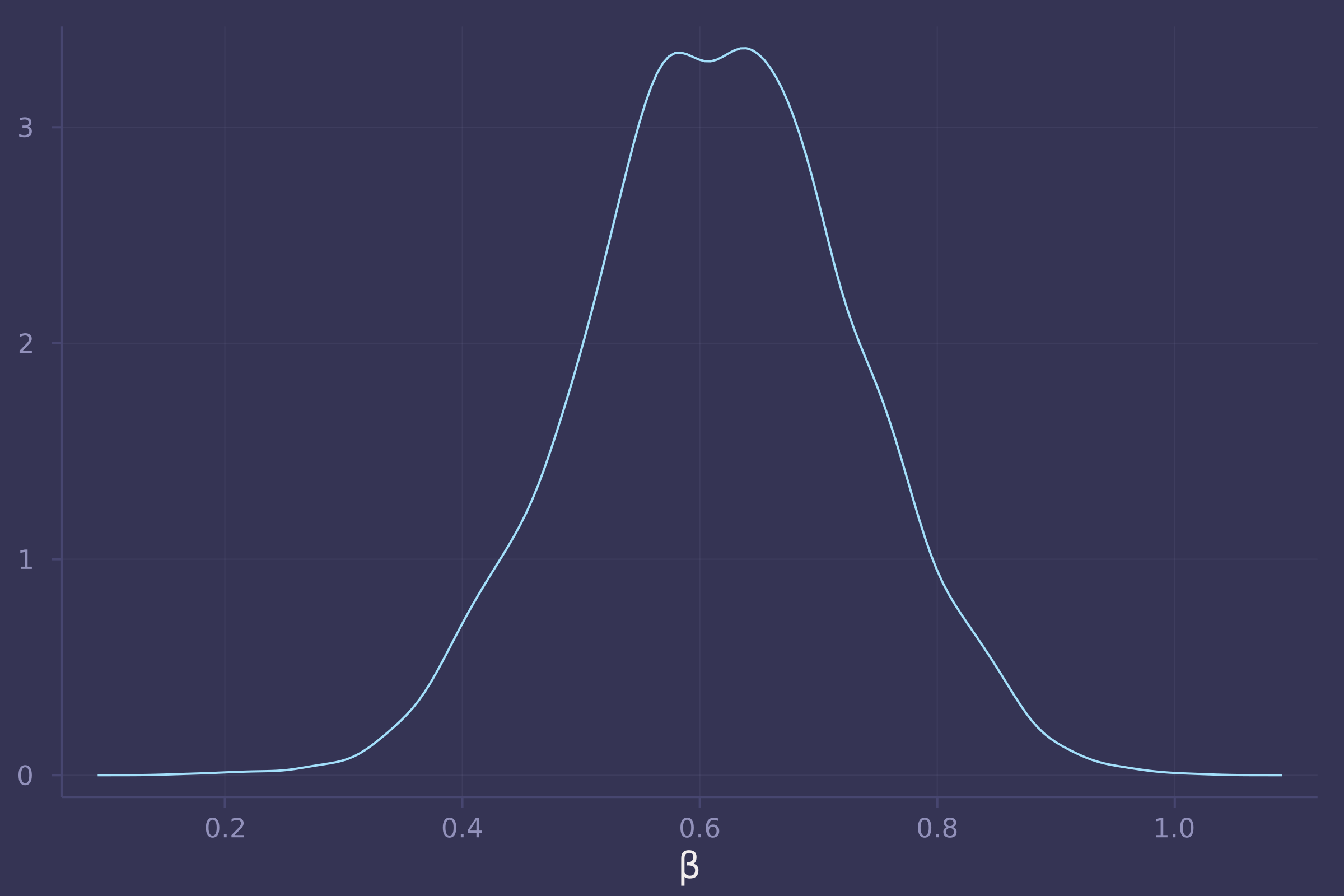
@model function bangladesh_urban_on_contraception_use_direct(c, u, d, a, k, n_districts)
σ ~ Exponential(1)
ᾱ ~ Normal(0, 1.5)
α ~ filldist(Normal(ᾱ, σ), n_districts)
β ~ Normal(0, 0.5)
γ ~ Normal(0, 0.5)
δ ~ Dirichlet(length(unique(k)), 2)
for i in 1:length(c)
c[i] ~ Bernoulli(invlogit(α[d[i]] + β * u[i] + γ * a[i] + δ[k[i]]))
end
end;
model_bangladesh_urban_on_contraception_use_direct = bangladesh_urban_on_contraception_use_direct(
bangladesh.use_contraception,
bangladesh.urban,
bangladesh.district,
standardize(bangladesh.age_centered),
bangladesh.living_children,
maximum(bangladesh.district)
);
post_bangladesh_urban_on_contraception_use_direct = sample(
model_bangladesh_urban_on_contraception_use_direct,
NUTS(),
5_000
);
density(post_bangladesh_urban_on_contraception_use_direct[:β], xlab="β", legend=false)
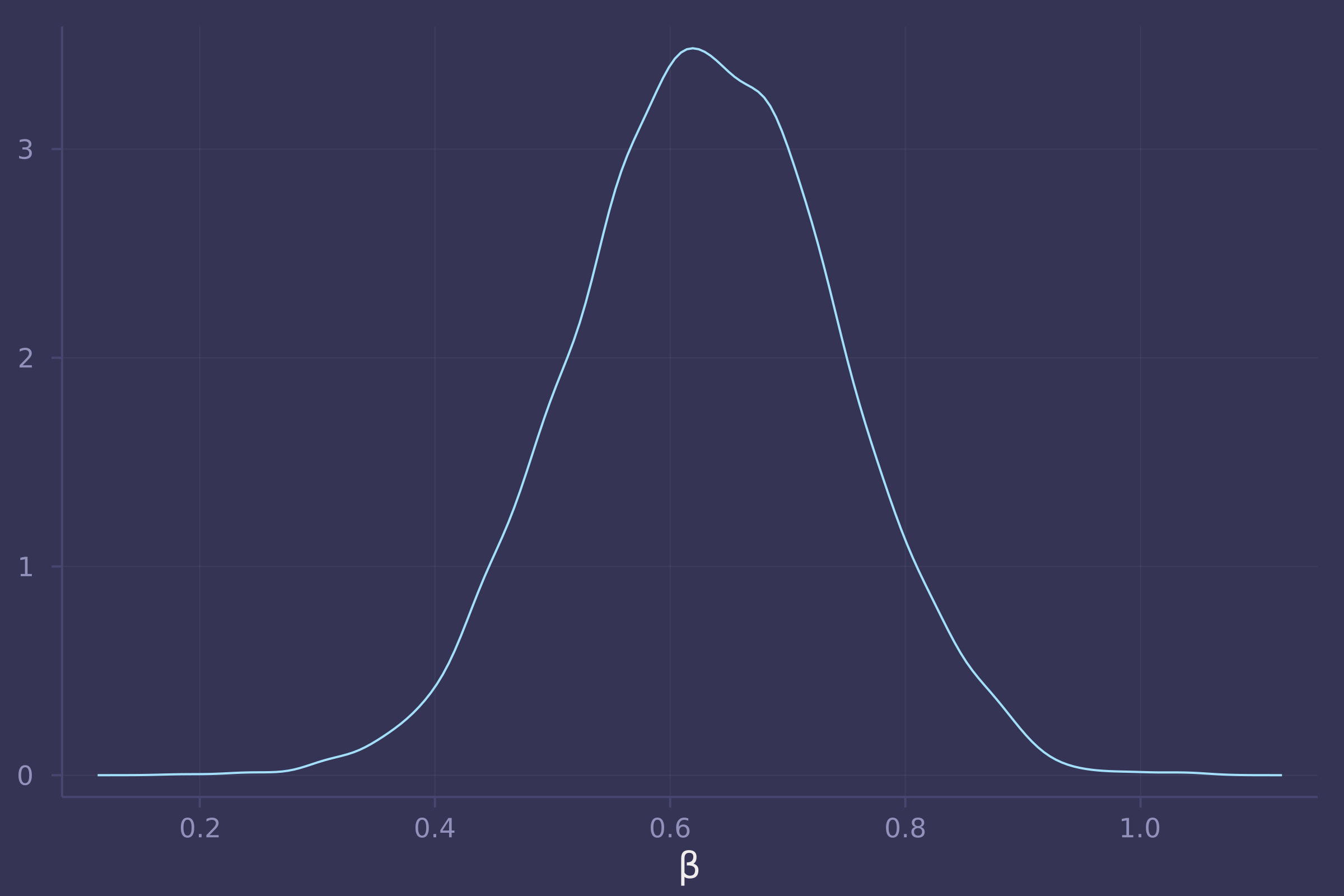
Homework 8
This assignment is difficult to complete without support for LKJCholesky in Turing.jl. There is an open issue to address this at github.com/TuringLang/Turing.jl/issues/1629.
invlogit(x) = 1 ./ (exp(-x) .+ 1);
monks = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/stat_rethinking_2022/main/homework/week08_Monks.csv"),
DataFrame
)
## 153×9 DataFrame
## Row │ dyad_id A B like_AB like_BA dislike_AB dislike_BA A_name ⋯
## │ Int64 Int64 Int64 Int64 Int64 Int64 Int64 String ⋯
## ─────┼──────────────────────────────────────────────────────────────────────────
## 1 │ 1 1 2 0 3 0 0 ROMUL ⋯
## 2 │ 2 1 3 3 3 0 0 ROMUL
## 3 │ 3 1 4 0 0 0 0 ROMUL
## 4 │ 4 1 5 0 0 0 0 ROMUL
## 5 │ 5 1 6 0 0 0 0 ROMUL ⋯
## 6 │ 6 1 7 0 0 0 0 ROMUL
## 7 │ 7 1 8 0 0 0 0 ROMUL
## 8 │ 8 1 9 0 0 0 1 ROMUL
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱
## 147 │ 147 14 18 0 0 0 0 ALBERT ⋯
## 148 │ 148 15 16 0 1 0 0 AMAND
## 149 │ 149 15 17 0 0 0 0 AMAND
## 150 │ 150 15 18 0 0 0 0 AMAND
## 151 │ 151 16 17 0 0 0 0 BASIL ⋯
## 152 │ 152 16 18 0 0 0 0 BASIL
## 153 │ 153 17 18 3 3 0 0 ELIAS
## 2 columns and 138 rows omitted
@model function monk_reciprocity(like_ab, like_ba, dyad_id, n_dyads)
σ ~ Exponential(1)
P ~ LKJ(2, 1)
d = Matrix(undef, n_dyads, 2)
for i in 1:n_dyads
d[i, :] = σ .* cholesky(P).L * randn(2)
end
α ~ Normal(0, 1)
p_ab = invlogit.(α .+ d[:, 1])
p_ba = invlogit.(α .+ d[:, 2])
like_ab .~ Binomial.(3, p_ab)
like_ba .~ Binomial.(3, p_ba)
end;
model_monk_reciprocity = monk_reciprocity(
monks.like_AB,
monks.like_BA,
monks.dyad_id,
nrow(monks)
);
@time post_monk_reciprocity = sample(model_monk_reciprocity, NUTS(), 500)
## 200.584295 seconds (2.73 G allocations: 283.401 GiB, 19.40% gc time, 0.01% compilation time)
## Chains MCMC chain (500×18×1 Array{Float64, 3}):
##
## Iterations = 251:1:750
## Number of chains = 1
## Samples per chain = 500
## Wall duration = 187.29 seconds
## Compute duration = 187.29 seconds
## parameters = σ, P[1,1], P[2,1], P[1,2], P[2,2], α
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat es ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## σ 0.3219 0.0000 0.0000 0.0000 2.0080 0.9980 ⋯
## P[1,1] 1.0000 0.0000 0.0000 0.0000 NaN NaN ⋯
## P[2,1] -0.5501 0.0000 0.0000 0.0000 NaN NaN ⋯
## P[1,2] -0.5501 0.0000 0.0000 0.0000 NaN NaN ⋯
## P[2,2] 1.0000 0.0000 0.0000 0.0000 2.0080 0.9980 ⋯
## α -1.8666 0.0000 0.0000 0.0000 2.0080 0.9980 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## σ 0.3219 0.3219 0.3219 0.3219 0.3219
## P[1,1] 1.0000 1.0000 1.0000 1.0000 1.0000
## P[2,1] -0.5501 -0.5501 -0.5501 -0.5501 -0.5501
## P[1,2] -0.5501 -0.5501 -0.5501 -0.5501 -0.5501
## P[2,2] 1.0000 1.0000 1.0000 1.0000 1.0000
## α -1.8666 -1.8666 -1.8666 -1.8666 -1.8666
Homework 9
trips = CSV.read(
download("https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/Achehunting.csv"),
DataFrame,
delim=';'
)
## 14364×8 DataFrame
## Row │ month day year id age kg.meat hours datatype
## │ Int64 Int64? Int64 Int64 Int64 Float64 Float64? Float64
## ───────┼───────────────────────────────────────────────────────────────────
## 1 │ 10 2 1981 3043 67 0.0 6.97 1.0
## 2 │ 10 3 1981 3043 67 0.0 9.0 1.0
## 3 │ 10 4 1981 3043 67 0.0 1.55 1.0
## 4 │ 10 5 1981 3043 67 4.5 8.0 1.0
## 5 │ 10 6 1981 3043 67 0.0 3.0 1.0
## 6 │ 10 7 1981 3043 67 0.0 7.5 1.0
## 7 │ 10 8 1981 3043 67 0.0 9.0 1.0
## 8 │ 2 6 1982 3043 68 0.0 7.3 1.0
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
## 14358 │ 8 26 2006 60121 21 4.96 missing 3.0
## 14359 │ 8 27 2006 60121 21 0.0 missing 3.0
## 14360 │ 2 2 2007 60121 22 0.0 missing 3.0
## 14361 │ 2 3 2007 60121 22 0.0 missing 3.0
## 14362 │ 2 21 2007 60121 22 0.0 missing 3.0
## 14363 │ 2 22 2007 60121 22 4.87 missing 3.0
## 14364 │ 3 5 2007 60121 22 3.15 missing 3.0
## 14349 rows omitted
rename!(trips, "kg.meat" => :kg_meat);
trips.success = convert.(Int, trips.kg_meat .> 0.);
@model function hunting1(s, a)
α ~ Beta(4, 4)
β ~ Exponential(2)
γ ~ Exponential(2)
δ ~ Exponential(0.5)
p = α .* exp.(-γ .* a) .* (1 .- exp.(-β .* a)) .^ δ
s .~ Bernoulli.(p)
end;
model_hunting1 = hunting1(trips.success, trips.age ./ maximum(trips.age));
@time post_hunting1 = sample(model_hunting1, NUTS(), 1_000)
## 70.565193 seconds (77.91 M allocations: 63.124 GiB, 2.56% gc time, 0.03% compilation time)
## Chains MCMC chain (1000×16×1 Array{Float64, 3}):
##
## Iterations = 501:1:1500
## Number of chains = 1
## Samples per chain = 1000
## Wall duration = 58.44 seconds
## Compute duration = 58.44 seconds
## parameters = α, β, γ, δ
## internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat e ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## α 0.8954 0.0403 0.0013 0.0019 392.0014 1.0021 ⋯
## β 7.0077 0.4904 0.0155 0.0233 349.7137 1.0053 ⋯
## γ 0.7696 0.0588 0.0019 0.0027 416.8462 1.0013 ⋯
## δ 5.4265 0.8002 0.0253 0.0358 364.8487 1.0034 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## α 0.8054 0.8704 0.9004 0.9244 0.9626
## β 6.0889 6.6834 6.9955 7.3301 7.9452
## γ 0.6362 0.7337 0.7785 0.8117 0.8707
## δ 3.9814 4.8914 5.3698 5.9156 7.2558
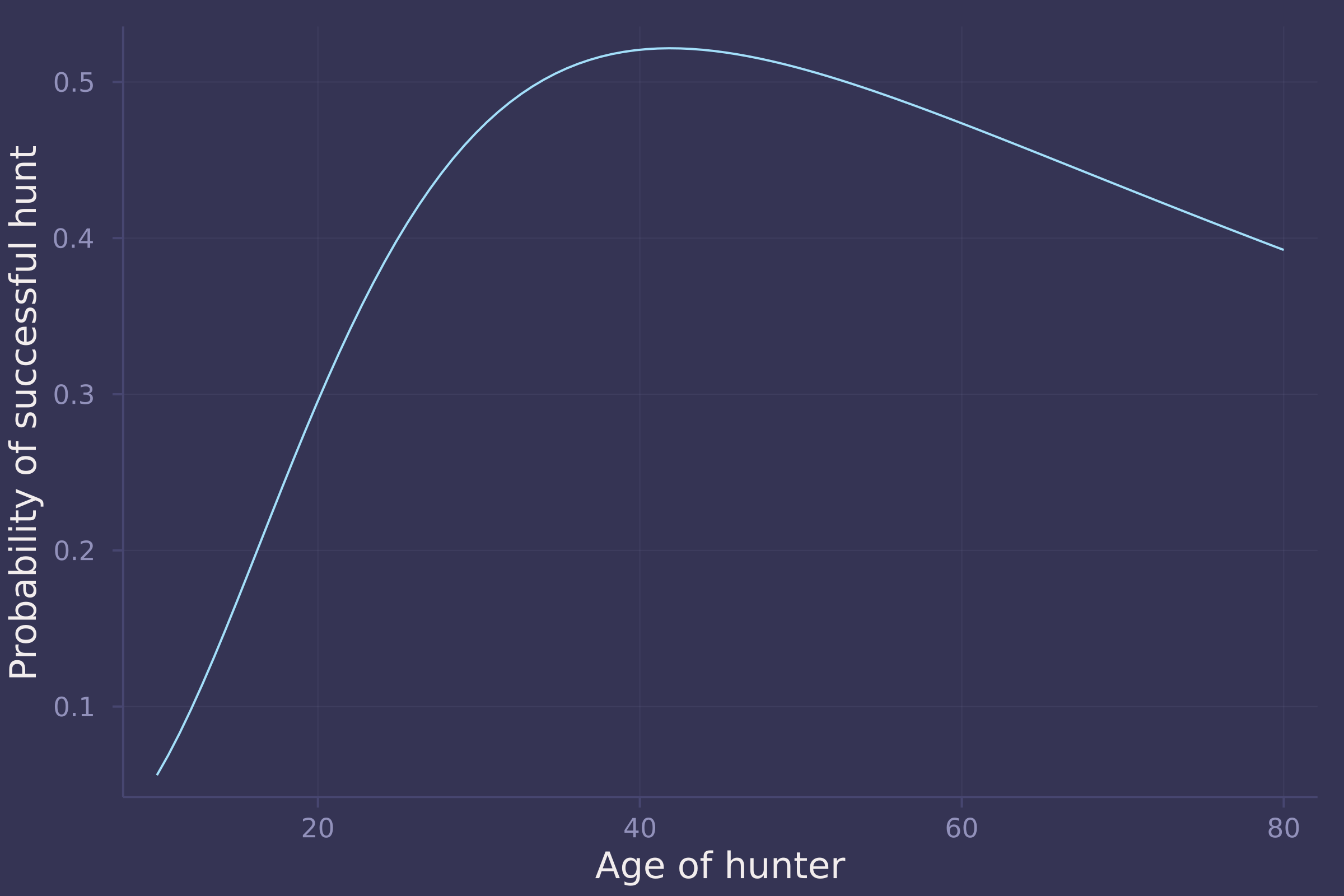
age_seq = collect(range(10, 80, length=100) ./ maximum(trips.age));
prob_success = vec(post_hunting1["α"]) .* exp.(-vec(post_hunting1["γ"]) * age_seq') .* (1 .- exp.(-post_hunting1["β"] * age_seq')) .^ post_hunting1["δ"];
mean_prob_success = vec(mean(prob_success, dims=1));
plot(age_seq .* maximum(trips.age), mean_prob_success, ylab="Probability of successful hunt", xlab="Age of hunter", legend=false)
@model function hunting2(s, a, hunter_id, n_hunters)
σ ~ Exponential(1)
τ ~ Exponential(1)
η ~ Exponential(1)
P ~ LKJ(2, η)
v = Matrix(undef, n_hunters, 2)
z ~ filldist(Normal(0, 1), 2, n_hunters)
D = diagm([σ, τ])
for i in 1:n_hunters
v[i, :] = D * cholesky(P).L * vec(z[:, i])
end
α ~ Beta(4, 4)
β ~ Normal(0, 0.5)
γ ~ Normal(0, 0.5)
δ ~ Exponential(0.5)
ε = exp.(β .+ vec(v[1:n_hunters, 1]))
ζ = exp.(γ .+ vec(v[1:n_hunters, 2]))
p = α .* exp.(-ζ[hunter_id] .* a) .* ((1 .- exp.(-ε[hunter_id] .* a)) .^ δ)
s .~ Bernoulli.(p)
end;
# reduce size of dataset for demonstration purposes!
trips2 = trips[1:111, :];
trips2.hunter_id = [findfirst(id .== unique(trips2.id)) for id in trips2.id];
model_hunting2 = hunting2(trips2.success, trips2.age ./ maximum(trips2.age), trips2.hunter_id, maximum(trips2.hunter_id));
post_hunting2 = sample(model_hunting2, NUTS(), 4000);
post_hunting2[["α", "β", "γ", "δ", "σ", "τ"]]
## Chains MCMC chain (4000×6×1 Array{Float64, 3}):
##
## Iterations = 1001:1:5000
## Number of chains = 1
## Samples per chain = 4000
## Wall duration = 63.85 seconds
## Compute duration = 63.85 seconds
## parameters = σ, τ, α, β, γ, δ
## internals =
##
## Summary Statistics
## parameters mean std naive_se mcse ess rhat ⋯
## Symbol Float64 Float64 Float64 Float64 Float64 Float64 ⋯
##
## σ 0.8937 0.8794 0.0139 0.0133 3643.9991 0.9998 ⋯
## τ 0.4947 0.4469 0.0071 0.0112 1647.0174 1.0003 ⋯
## α 0.5722 0.1218 0.0019 0.0024 3251.8017 0.9998 ⋯
## β 0.0744 0.4869 0.0077 0.0082 3560.4339 1.0006 ⋯
## γ -0.2992 0.3665 0.0058 0.0072 2742.6807 0.9998 ⋯
## δ 0.3093 0.3012 0.0048 0.0054 3243.0843 0.9998 ⋯
## 1 column omitted
##
## Quantiles
## parameters 2.5% 25.0% 50.0% 75.0% 97.5%
## Symbol Float64 Float64 Float64 Float64 Float64
##
## σ 0.0202 0.2604 0.6226 1.2457 3.2864
## τ 0.0167 0.1760 0.3842 0.6886 1.5920
## α 0.3540 0.4824 0.5651 0.6600 0.8156
## β -0.9074 -0.2477 0.0736 0.3976 1.0232
## γ -1.0965 -0.5331 -0.2765 -0.0409 0.3427
## δ 0.0063 0.0886 0.2202 0.4376 1.0983
Updated January 27, 2022 with Homework 1 and Homework 2 solutions
Updated February 10, 2022 with Homework 3 solutions
Updated February 24, 2022 with Homework 4 solutions
Updated March 10, 2022 with Homework 5 solutions
Updated March 24, 2022 with Homework 6 solutions
Updated April 7, 2022 with Homework 7 solutions
Updated April 21, 2022 with Homework 8 solutions
Updated May 5, 2022 with Homework 9 solutions